આકૃતિમાં દર્શાવ્યા મુજબ $ T $ આકારનો પદાર્થ લીસી સપાટી પર છે. હવે બિંદુ $ P $ પર,$ AB $ ને સમાંતર દિશામાં બળ $\mathop F\limits^ \to $ એવી રીતે લગાવવામાં આવે છે, જેથી પદાર્થ ચાકગતિ કર્યા વિના ફક્ત રેખીય ગતિ કરે, તો બિંદુ $ C$ ની સાપેક્ષે બિંદુ $P$ નું સ્થાન શોધો.
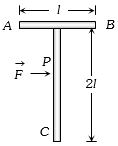
આકૃતિમાં દર્શાવ્યા મુજબ $ T $ આકારનો પદાર્થ લીસી સપાટી પર છે. હવે બિંદુ $ P $ પર,$ AB $ ને સમાંતર દિશામાં બળ $\mathop F\limits^ \to $ એવી રીતે લગાવવામાં આવે છે, જેથી પદાર્થ ચાકગતિ કર્યા વિના ફક્ત રેખીય ગતિ કરે, તો બિંદુ $ C$ ની સાપેક્ષે બિંદુ $P$ નું સ્થાન શોધો.

- [AIEEE 2005]
- A
$\frac{4l}{3}$
- B
$l$
- C
$\frac{2l}{3}$
- D
$\frac{3l}{2}$
Similar Questions
$1 \,\,g, 2 \,\,g$ અને $3\,\, g$ દળ ધરાવતા કણોથી બનેલા તંત્રનું દ્રવ્યમાન કેન્દ્ર ઊગમબિંદુ પર છે. $4 \,\,g$ દળ અને $\alpha (\hat i + 2\hat j + 3\hat k)$ સ્થાનસદિશ ધરાવતા કણને સામેલ કરતાં તંત્રના દ્રવ્યમાન કેન્દ્રના યામ $(1, 2, 3)$ મળે છે. જો અચળ હોય, તો તેનું મૂલ્ય ..... હોવું જોઈએ.
$1 \,\,g, 2 \,\,g$ અને $3\,\, g$ દળ ધરાવતા કણોથી બનેલા તંત્રનું દ્રવ્યમાન કેન્દ્ર ઊગમબિંદુ પર છે. $4 \,\,g$ દળ અને $\alpha (\hat i + 2\hat j + 3\hat k)$ સ્થાનસદિશ ધરાવતા કણને સામેલ કરતાં તંત્રના દ્રવ્યમાન કેન્દ્રના યામ $(1, 2, 3)$ મળે છે. જો અચળ હોય, તો તેનું મૂલ્ય ..... હોવું જોઈએ.
ત્રણ સમાન દળને $ (0,0), (a,0)$ અને $\left( {\frac{a}{2}\,,\frac{{a\sqrt 3 }}{2}} \right)$ પર મૂકવામાં આવે છે. દ્રવ્યમાન કેન્દ્રના યામાક્ષ શોધો.
ત્રણ સમાન દળને $ (0,0), (a,0)$ અને $\left( {\frac{a}{2}\,,\frac{{a\sqrt 3 }}{2}} \right)$ પર મૂકવામાં આવે છે. દ્રવ્યમાન કેન્દ્રના યામાક્ષ શોધો.
કાર્બન મોનોક્સાઈડ અણુઓમાં, કાર્બન અને ઓક્સીજન અણુઓને $1.2 \,\mathring A$ અંતર જેટલાં અલગ કરવામાં આવે છે. કાર્બન અણુથી. દ્રવ્યમાન કેન્દ્રનું અંતર .......... $\mathring A$ હશે?
કાર્બન મોનોક્સાઈડ અણુઓમાં, કાર્બન અને ઓક્સીજન અણુઓને $1.2 \,\mathring A$ અંતર જેટલાં અલગ કરવામાં આવે છે. કાર્બન અણુથી. દ્રવ્યમાન કેન્દ્રનું અંતર .......... $\mathring A$ હશે?
વ્હીલને તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષને અનુલક્ષીને નિયમિત ગતિ કરતું તથા યાંત્રિક (રેખીય અને ચાકગતિ) સંતુલનમાં છે તેમ ધારો. કારણ કે તેની ગતિ જાળવી રાખવા બહારથી કોઈ બાહ્યબળ કે ટોર્કની જરૂર નથી. છતાં વ્હીલનાં કણો કેન્દ્ર તરફ કેન્દ્રગામી પ્રવેગ અનુભવે છે. વ્હીલના સંતુલન સાથે આ હકીકતની સમજૂતી કેવી રીતે કરશો ? અડધા વ્હીલને તેના દ્રવ્યમાન કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષને અનુલક્ષીને નિયમિત ગતિમાં કેવી રીતે ગોઠવશો ? આ ગતિ જાળવી રાખવા બાહ્યબળની જરૂર પડશે ?
વ્હીલને તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષને અનુલક્ષીને નિયમિત ગતિ કરતું તથા યાંત્રિક (રેખીય અને ચાકગતિ) સંતુલનમાં છે તેમ ધારો. કારણ કે તેની ગતિ જાળવી રાખવા બહારથી કોઈ બાહ્યબળ કે ટોર્કની જરૂર નથી. છતાં વ્હીલનાં કણો કેન્દ્ર તરફ કેન્દ્રગામી પ્રવેગ અનુભવે છે. વ્હીલના સંતુલન સાથે આ હકીકતની સમજૂતી કેવી રીતે કરશો ? અડધા વ્હીલને તેના દ્રવ્યમાન કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષને અનુલક્ષીને નિયમિત ગતિમાં કેવી રીતે ગોઠવશો ? આ ગતિ જાળવી રાખવા બાહ્યબળની જરૂર પડશે ?
$r $ ત્રિજ્યાવાળા સમાન પ્રકારના ત્રણ દડાઓ એકબીજાને અડે તેમ સમક્ષિતિજ સપાટી પર મૂકેલા છે. આ દડા એવી રીતે ગોઠવેલા છે, જેથી તેમના દ્રવ્યમાન-કેન્દ્રને જોડતા તેઓ સમબાજુ ત્રિકોણ બનાવે. આ તંત્રનું દ્રવ્યમાન-કેન્દ્ર ........ હશે.
$r $ ત્રિજ્યાવાળા સમાન પ્રકારના ત્રણ દડાઓ એકબીજાને અડે તેમ સમક્ષિતિજ સપાટી પર મૂકેલા છે. આ દડા એવી રીતે ગોઠવેલા છે, જેથી તેમના દ્રવ્યમાન-કેન્દ્રને જોડતા તેઓ સમબાજુ ત્રિકોણ બનાવે. આ તંત્રનું દ્રવ્યમાન-કેન્દ્ર ........ હશે.
