A $T$ shaped object with dimensions shown in the figure, is lying a smooth floor. A force $'\vec F'$ is applied at the point $P$ parallel to $AB,$ such that the object has only the translational motion without rotation. Find the location of $P$ with respect to $C$
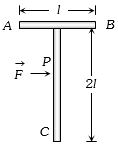
A $T$ shaped object with dimensions shown in the figure, is lying a smooth floor. A force $'\vec F'$ is applied at the point $P$ parallel to $AB,$ such that the object has only the translational motion without rotation. Find the location of $P$ with respect to $C$

- [AIEEE 2005]
- A
$\frac{4l}{3}$
- B
$l$
- C
$\frac{2l}{3}$
- D
$\frac{3l}{2}$
Similar Questions
Two objects of mass $10\,kg$ and $20\,kg$ respectively are connected to the two ends of a rigid rod of length $10\,m$ with negligible mass. The distance of the center of mass of the system from the $10\,kg$ mass is :
Two objects of mass $10\,kg$ and $20\,kg$ respectively are connected to the two ends of a rigid rod of length $10\,m$ with negligible mass. The distance of the center of mass of the system from the $10\,kg$ mass is :
- [NEET 2022]
Two bodies of mass $1\,kg$ and $3\,kg$ have position vectors $\hat{i}+2 \hat{j}+\hat{k}$ and $-3 \hat{i}-2 \hat{j}+\hat{k}$ respectively.The magnitude of position vector of centre of mass of this system will be similar to the magnitude of vector.
- [AIPMT 2009]
A firecracker is thrown with velocity of $30 \,ms ^{-1}$ in a direction which makes an angle of $75^{\circ}$ with the vertical axis. At some point on its trajectory, the firecracker splits into two identical pieces in such a way that one piece falls $27 \,m$ far from the shooting point. Assuming that all trajectories are contained in the same plane, how far will the other piece fall from the shooting point? (Take, $g=10 \,ms ^{-2}$ and neglect air resistance)
A firecracker is thrown with velocity of $30 \,ms ^{-1}$ in a direction which makes an angle of $75^{\circ}$ with the vertical axis. At some point on its trajectory, the firecracker splits into two identical pieces in such a way that one piece falls $27 \,m$ far from the shooting point. Assuming that all trajectories are contained in the same plane, how far will the other piece fall from the shooting point? (Take, $g=10 \,ms ^{-2}$ and neglect air resistance)
- [KVPY 2012]
As shown in figure, when a spherical cavity (centred at $\mathrm{O})$ of radius $1$ is cut out of a uniform sphere of radius $\mathrm{R} \text { (centred at } \mathrm{C}),$ the centre of mass of remaining (shaded) part of sphere is at $G$, i.e, on the surface of the cavity. $\mathrm{R}$ can be detemined by the equation
As shown in figure, when a spherical cavity (centred at $\mathrm{O})$ of radius $1$ is cut out of a uniform sphere of radius $\mathrm{R} \text { (centred at } \mathrm{C}),$ the centre of mass of remaining (shaded) part of sphere is at $G$, i.e, on the surface of the cavity. $\mathrm{R}$ can be detemined by the equation
- [JEE MAIN 2020]
Two masses $m_1$ and $m_2$ ($m_1$ > $m_2$) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of center of mass is
Two masses $m_1$ and $m_2$ ($m_1$ > $m_2$) are connected by massless flexible and inextensible string passed over massless and frictionless pulley. The acceleration of center of mass is
