एकसमान पृष्ठीय आवेश घनत्व $\sigma_{+}$व $\sigma_{-}$वाली दो आवेशित पतली अनन्त लम्बी समतलीय शीटों पर विचार कीजिये जहाँ $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$है, तथा ये आपस में समकोण पर प्रतिच्छेदित करती है। इस निकाय के लिये विधुत क्षेत्र रेखाओं का सर्वाधिक सही चित्रण होगा:-
एकसमान पृष्ठीय आवेश घनत्व $\sigma_{+}$व $\sigma_{-}$वाली दो आवेशित पतली अनन्त लम्बी समतलीय शीटों पर विचार कीजिये जहाँ $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$है, तथा ये आपस में समकोण पर प्रतिच्छेदित करती है। इस निकाय के लिये विधुत क्षेत्र रेखाओं का सर्वाधिक सही चित्रण होगा:-
- [JEE MAIN 2020]
- A

- B
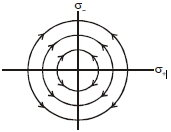
- C

- D

Similar Questions
गॉस नियम सत्य है यदि किसी आवेश के कारण विद्युत क्षेत्र दूरी $r$ के साथ निम्न प्रकार परिवर्तित हो
गॉस नियम सत्य है यदि किसी आवेश के कारण विद्युत क्षेत्र दूरी $r$ के साथ निम्न प्रकार परिवर्तित हो
तीन समान धन आवेश $q$ एक समबाहु त्रिभुज के शीर्षों पर रखे हैं परिणामी विद्युत बल रेखाऐं निम्न प्रकार से खींची जा सकती है
तीन समान धन आवेश $q$ एक समबाहु त्रिभुज के शीर्षों पर रखे हैं परिणामी विद्युत बल रेखाऐं निम्न प्रकार से खींची जा सकती है
- [IIT 2001]
मूलबिन्दु पर अवस्थित $2 \times 10^{-9}\, m ^{3}$ के किसी वार्धिक आयतन में परिबद्ध कुल आवेश $......\,nC$ होगा, यदि इसके क्षेत्र का विधुत फ्लक्स घनत्व $D = e ^{- x } \sin y \hat{ i }- e ^{- x } \cos y \hat{ j }+2 z \hat{ k } C / m ^{2}$ पाया जाता है।
मूलबिन्दु पर अवस्थित $2 \times 10^{-9}\, m ^{3}$ के किसी वार्धिक आयतन में परिबद्ध कुल आवेश $......\,nC$ होगा, यदि इसके क्षेत्र का विधुत फ्लक्स घनत्व $D = e ^{- x } \sin y \hat{ i }- e ^{- x } \cos y \hat{ j }+2 z \hat{ k } C / m ^{2}$ पाया जाता है।
- [JEE MAIN 2021]
किसी काले बॉक्स के पृष्ठ पर विध्यूत क्षेत्र की सावधानीपूर्वक ली गई माप यह संकेत देती है कि बॉक्स के पृष्ठ से गुजरने वाला नेट फ्लक्स $8.0 \times 10^{3}\, Nm ^{2} / C$ है।
$(a)$ बॉक्स के भीतर नेट आवेश कितना है?
$(b)$ यद् बॉंक्स के पृष्ठ से नेट बहिर्मुखी फ्लक्स शून्य है तो क्या आप यह निष्कर्ष निकालेंगे कि बॉक्स के भीतर कोई आवेश नहीं है? क्यों, अथवा क्यों नहीं?
किसी काले बॉक्स के पृष्ठ पर विध्यूत क्षेत्र की सावधानीपूर्वक ली गई माप यह संकेत देती है कि बॉक्स के पृष्ठ से गुजरने वाला नेट फ्लक्स $8.0 \times 10^{3}\, Nm ^{2} / C$ है।
$(a)$ बॉक्स के भीतर नेट आवेश कितना है?
$(b)$ यद् बॉंक्स के पृष्ठ से नेट बहिर्मुखी फ्लक्स शून्य है तो क्या आप यह निष्कर्ष निकालेंगे कि बॉक्स के भीतर कोई आवेश नहीं है? क्यों, अथवा क्यों नहीं?
किसी क्षेत्र में विधुत क्षेत्र को इस प्रकार दर्शाया गया है- $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{ i }+\frac{4}{5} E _{0} \hat{ j }\right) \frac{ N }{ C }$ है। $0.2\, m ^{2}$ क्षेत्रफल के आयताकार पष्ठ $\left( y - z\right.$ तल के समान्तर) और $0.3 \,m ^{2}$ के पष्ठ $( x - z$ तल के समान्तर $)$ से गुजरने वाले दिए गये क्षेत्र के फ्लक्स का अनुपात $a : b$ है। यहाँ $a =\ldots$ है। [यहाँ $\hat{ i }, \hat{ j }$ और $\hat{ k }$ क्रमशः $x , y$ और $z$-अक्ष के अनुदिश एकांक सदिश है]
किसी क्षेत्र में विधुत क्षेत्र को इस प्रकार दर्शाया गया है- $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{ i }+\frac{4}{5} E _{0} \hat{ j }\right) \frac{ N }{ C }$ है। $0.2\, m ^{2}$ क्षेत्रफल के आयताकार पष्ठ $\left( y - z\right.$ तल के समान्तर) और $0.3 \,m ^{2}$ के पष्ठ $( x - z$ तल के समान्तर $)$ से गुजरने वाले दिए गये क्षेत्र के फ्लक्स का अनुपात $a : b$ है। यहाँ $a =\ldots$ है। [यहाँ $\hat{ i }, \hat{ j }$ और $\hat{ k }$ क्रमशः $x , y$ और $z$-अक्ष के अनुदिश एकांक सदिश है]
- [JEE MAIN 2021]
