બે પાતળી વિધુતભારિત સમતલ સપાટીની $\sigma_{+}$ પુષ્ઠ ધનતા અને $\sigma_{-}$ છે. જયા $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$ બંને સમતલ લંબ છેદે છે. તો તંત્રની વિધુતક્ષેત્ર રેખાનું નિરૂપણ
બે પાતળી વિધુતભારિત સમતલ સપાટીની $\sigma_{+}$ પુષ્ઠ ધનતા અને $\sigma_{-}$ છે. જયા $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$ બંને સમતલ લંબ છેદે છે. તો તંત્રની વિધુતક્ષેત્ર રેખાનું નિરૂપણ
- [JEE MAIN 2020]
- A

- B
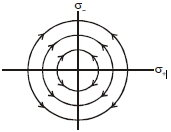
- C

- D

Similar Questions
આકૃતિમાં દર્શાવ્યા મુજબ $'q'$ વિજભાર ને સમઘનનાં એક ખૂણા પર ગોઠવવામાં આવ્યો છે. આચ્છાદિત ક્ષેત્રફળમાંથી પસાર થતાં સ્થિત વીજ ક્ષેત્ર $\overrightarrow{ E }$ નું ફ્લક્સ ...... હશે.
આકૃતિમાં દર્શાવ્યા મુજબ $'q'$ વિજભાર ને સમઘનનાં એક ખૂણા પર ગોઠવવામાં આવ્યો છે. આચ્છાદિત ક્ષેત્રફળમાંથી પસાર થતાં સ્થિત વીજ ક્ષેત્ર $\overrightarrow{ E }$ નું ફ્લક્સ ...... હશે.
- [JEE MAIN 2021]
આકૃતિમાં $q_1$ અને $q_2$ બે વિદ્યુતભારને કારણે વિદ્યુતક્ષેત્રરેખા દર્શાવે છે. બે વિદ્યુતભારની સંજ્ઞા કેવી હશે?
આકૃતિમાં $q_1$ અને $q_2$ બે વિદ્યુતભારને કારણે વિદ્યુતક્ષેત્રરેખા દર્શાવે છે. બે વિદ્યુતભારની સંજ્ઞા કેવી હશે?
- [AIPMT 1994]
$\overrightarrow{\mathrm{E}}=\frac{2 \hat{i}+6 \hat{j}+8 \hat{k}}{\sqrt{6}}$ થી રજૂ થતું વિદ્યુતક્ષેત્ર $4 \mathrm{~m}^2$ ક્ષેત્રફળ અને $\hat{n}=\left(\frac{2 \hat{i}+\hat{j}+\hat{k}}{\sqrt{6}}\right)$ જેટલો એકમ સદિશ ધરાવતી સપાટીમાંથી પસાર થાય છે. સપાટી સાથે સંકળાયેલ વિદ્યુત ફ્લક્સ. . . . . .$Vm$ હશે.
$\overrightarrow{\mathrm{E}}=\frac{2 \hat{i}+6 \hat{j}+8 \hat{k}}{\sqrt{6}}$ થી રજૂ થતું વિદ્યુતક્ષેત્ર $4 \mathrm{~m}^2$ ક્ષેત્રફળ અને $\hat{n}=\left(\frac{2 \hat{i}+\hat{j}+\hat{k}}{\sqrt{6}}\right)$ જેટલો એકમ સદિશ ધરાવતી સપાટીમાંથી પસાર થાય છે. સપાટી સાથે સંકળાયેલ વિદ્યુત ફ્લક્સ. . . . . .$Vm$ હશે.
- [JEE MAIN 2024]
$1$ કુલંબનો વિદ્યુતભાર $10 \,cm$ ત્રિજ્યાના ગોળાના અને $20 \,cm$ બાજુના સમઘનના કેન્દ્ર પાસે રહેલો છે. ગોળા અને સમઘનમાંથી બહાર જતા ફલક્સનો ગુણોત્તર
$1$ કુલંબનો વિદ્યુતભાર $10 \,cm$ ત્રિજ્યાના ગોળાના અને $20 \,cm$ બાજુના સમઘનના કેન્દ્ર પાસે રહેલો છે. ગોળા અને સમઘનમાંથી બહાર જતા ફલક્સનો ગુણોત્તર
$20\ cm$ બાજુઓનો ચોરસ $80\ cm$ ત્રિજ્યાના ગોળાના પૃષ્ઠ વડે ઘેરાયેલો છે. ચોરસ અને ગોળાના કેન્દ્રો સમાન છે. ચાર વિદ્યુતભારો $2 \times 10^{-6} C, -5 \times 10^{-6}\ C$, $-3 \times 10^{-6}\ C, 6 \times 10^{-6}\ C$ ને ચોરસના ચાર ખૂણા આગળ મૂકેલા છે. ગોળીય પૃષ્ઠમાંથી બહાર આવતું કુલ ફલક્સ $Nm^2/C$ માં ....... હશે.
$20\ cm$ બાજુઓનો ચોરસ $80\ cm$ ત્રિજ્યાના ગોળાના પૃષ્ઠ વડે ઘેરાયેલો છે. ચોરસ અને ગોળાના કેન્દ્રો સમાન છે. ચાર વિદ્યુતભારો $2 \times 10^{-6} C, -5 \times 10^{-6}\ C$, $-3 \times 10^{-6}\ C, 6 \times 10^{-6}\ C$ ને ચોરસના ચાર ખૂણા આગળ મૂકેલા છે. ગોળીય પૃષ્ઠમાંથી બહાર આવતું કુલ ફલક્સ $Nm^2/C$ માં ....... હશે.
