Two charged thin infinite plane sheets of uniform surface charge density $\sigma_{+}$ and $\sigma_{-}$ where $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$ intersect at right angle. Which of the following best represents the electric field lines for this system
Two charged thin infinite plane sheets of uniform surface charge density $\sigma_{+}$ and $\sigma_{-}$ where $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$ intersect at right angle. Which of the following best represents the electric field lines for this system
- [JEE MAIN 2020]
- A
- B
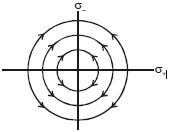
- C
- D
Similar Questions
For a given surface the Gauss's law is stated as $\oint {E \cdot ds} = 0$. From this we can conclude that
For a given surface the Gauss's law is stated as $\oint {E \cdot ds} = 0$. From this we can conclude that
What is the net flux of the uniform electric field of $E =3 \times 10^{3} i\; N / C $ through a cube of side $20\; cm$ oriented so that its faces are parallel to the coordinate planes?
What is the net flux of the uniform electric field of $E =3 \times 10^{3} i\; N / C $ through a cube of side $20\; cm$ oriented so that its faces are parallel to the coordinate planes?
When electric flux is said to be positive, negative or zero ?
When electric flux is said to be positive, negative or zero ?
A long cylindrical volume contains a uniformly distributed charge of density $\rho$. The radius of cylindrical volume is $R$. A charge particle $(q)$ revolves around the cylinder in a circular path. The kinetic of the particle is
A long cylindrical volume contains a uniformly distributed charge of density $\rho$. The radius of cylindrical volume is $R$. A charge particle $(q)$ revolves around the cylinder in a circular path. The kinetic of the particle is
- [JEE MAIN 2022]
The electric flux for Gaussian surface A that enclose the charged particles in free space is (given $q_1$ = $-14\, nC$, $q_2$ = $78.85\, nC$, $q_3$ = $-56 \,nC$)
The electric flux for Gaussian surface A that enclose the charged particles in free space is (given $q_1$ = $-14\, nC$, $q_2$ = $78.85\, nC$, $q_3$ = $-56 \,nC$)