$1.25 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$ घनत्व वाली ग्लिसरीन, एक नली के शंक्वाकार भाग में प्रवाहित हो रही है। नली के अंतिम सिरों के अनुप्रस्थ काट का क्षेत्रफल $10 \mathrm{~cm}^2$ एवं $5 \mathrm{~cm}^2$ है, एवं इसके सिरों पर दाबान्तर $3 \mathrm{Nm}^{-2}$ है। नली के अन्दर ग्लिसरीन के प्रवाह की दर $\mathrm{x} \times 10^{-5} \mathrm{~m}^3 \mathrm{~s}^{-1}$ है। $\mathrm{x}$ का मान_______________ है।
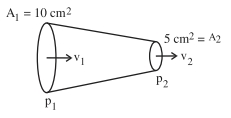
$1.25 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$ घनत्व वाली ग्लिसरीन, एक नली के शंक्वाकार भाग में प्रवाहित हो रही है। नली के अंतिम सिरों के अनुप्रस्थ काट का क्षेत्रफल $10 \mathrm{~cm}^2$ एवं $5 \mathrm{~cm}^2$ है, एवं इसके सिरों पर दाबान्तर $3 \mathrm{Nm}^{-2}$ है। नली के अन्दर ग्लिसरीन के प्रवाह की दर $\mathrm{x} \times 10^{-5} \mathrm{~m}^3 \mathrm{~s}^{-1}$ है। $\mathrm{x}$ का मान_______________ है।

- [JEE MAIN 2023]
- A
$2$
- B
$6$
- C
$8$
- D
$4$
Similar Questions
एक लम्बा बेलनाकार पात्र द्रव से आधा भरा हुआ है। जब पात्र को इसकी स्वयं की ऊर्ध्वाधर अक्ष के सापेक्ष घुमाया जाता है तो द्रव दीवार के नजदीक ऊपर की ओर चढ़ता है। यदि पात्र की त्रिज्या $5\, cm$ हो तथा इसकी घूर्णन चाल $2$ घूर्णन प्रति सेकण्ड हो तो केन्द्र तथा इसकी साइडों की ऊँचाई में $cm$ में अन्तर होगा?
एक लम्बा बेलनाकार पात्र द्रव से आधा भरा हुआ है। जब पात्र को इसकी स्वयं की ऊर्ध्वाधर अक्ष के सापेक्ष घुमाया जाता है तो द्रव दीवार के नजदीक ऊपर की ओर चढ़ता है। यदि पात्र की त्रिज्या $5\, cm$ हो तथा इसकी घूर्णन चाल $2$ घूर्णन प्रति सेकण्ड हो तो केन्द्र तथा इसकी साइडों की ऊँचाई में $cm$ में अन्तर होगा?
- [JEE MAIN 2019]
बर्नूली समीकरण के अनुप्रयोग में यदि निरपेक्ष दाब के स्थान पर प्रमापी दाब (गेज़ दाब) का प्रयोग करें तो क्या इससे कोई अंतर पडेगा ? स्पष्ट कीजिए ।
बर्नूली समीकरण के अनुप्रयोग में यदि निरपेक्ष दाब के स्थान पर प्रमापी दाब (गेज़ दाब) का प्रयोग करें तो क्या इससे कोई अंतर पडेगा ? स्पष्ट कीजिए ।
चित्र क्षैतिजत: गतिशील वायुयान के पंखों की ऊध्र्वाधर काट प्रदर्शित करता है। किस स्थिति में ऊपर की ओर एक बल कार्य करेगा
चित्र क्षैतिजत: गतिशील वायुयान के पंखों की ऊध्र्वाधर काट प्रदर्शित करता है। किस स्थिति में ऊपर की ओर एक बल कार्य करेगा
वायुयान के पंख के ऊपर व नीचे से वायु क्रमश: $120 m/s$ व $90 m/s$ के क्षैतिज वेग से बह रही है। वायु का घनत्व $ 1.3 kg / m^3$ है। पंख की लम्बाई $10 m$ व औसत चौड़ाई $2 m$ है। पंख के दोनों ओर दाबांतर ........ पास्कल होगा
वायुयान के पंख के ऊपर व नीचे से वायु क्रमश: $120 m/s$ व $90 m/s$ के क्षैतिज वेग से बह रही है। वायु का घनत्व $ 1.3 kg / m^3$ है। पंख की लम्बाई $10 m$ व औसत चौड़ाई $2 m$ है। पंख के दोनों ओर दाबांतर ........ पास्कल होगा
एक आदर्श द्रव जिसका घनत्व $800\,kgm ^{-3}$ है, अनुप्रस्थ काट क्षैत्रफल $a$ से $\frac{ a }{2}$ वाले मुड़े हुए पाईप से बिना घर्पण बहता है। पाईप के चौड़े एवं संकरे भाग के मध्य दाबांतर $4100\,Pa$ है। यदि चौड़े क्षेत्रफल पर द्रव का वेग $\frac{\sqrt{ x }}{6} ms ^{-1}$ है, तो $x$ का मान ज्ञात कीजिए। $\left( g =10 m ^{-2}\right)$
एक आदर्श द्रव जिसका घनत्व $800\,kgm ^{-3}$ है, अनुप्रस्थ काट क्षैत्रफल $a$ से $\frac{ a }{2}$ वाले मुड़े हुए पाईप से बिना घर्पण बहता है। पाईप के चौड़े एवं संकरे भाग के मध्य दाबांतर $4100\,Pa$ है। यदि चौड़े क्षेत्रफल पर द्रव का वेग $\frac{\sqrt{ x }}{6} ms ^{-1}$ है, तो $x$ का मान ज्ञात कीजिए। $\left( g =10 m ^{-2}\right)$
- [JEE MAIN 2022]
