Glycerine of density $1.25 \times 10^3\,kg\,m ^{-3}$ is flowing through the conical section of pipe. The area of cross-section of the pipe at its ends is $10\,cm ^2$ and $5\,cm ^2$ and pressure drop across its length is $3\,Nm ^{-2}$. The rate of flow of glycerine through the pipe is $x \times 10^{-5} m ^3 s ^{-1}$. The value of $x$ is $..............$.
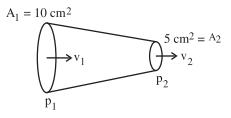
Glycerine of density $1.25 \times 10^3\,kg\,m ^{-3}$ is flowing through the conical section of pipe. The area of cross-section of the pipe at its ends is $10\,cm ^2$ and $5\,cm ^2$ and pressure drop across its length is $3\,Nm ^{-2}$. The rate of flow of glycerine through the pipe is $x \times 10^{-5} m ^3 s ^{-1}$. The value of $x$ is $..............$.

- [JEE MAIN 2023]
- A
$2$
- B
$6$
- C
$8$
- D
$4$
Similar Questions
Consider a water jar of radius $R$ that has water filled up to height $H$ and is kept on a stand of height $h$ (see figure) . Through a hole of radius $r$ $(r << R)$ at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is $x.$ Then
Consider a water jar of radius $R$ that has water filled up to height $H$ and is kept on a stand of height $h$ (see figure) . Through a hole of radius $r$ $(r << R)$ at its bottom, the water leaks out and the stream of water coming down towards the ground has a shape like a funnel as shown in the figure. If the radius of the cross-section of water stream when it hits the ground is $x.$ Then
- [JEE MAIN 2016]
Given below are two statements :
Statement $I$ : When speed of liquid is zero everywhere, pressure difference at any two points depends on equation $\mathrm{P}_1-\mathrm{P}_2=\rho \mathrm{g}\left(\mathrm{h}_2-\mathrm{h}_1\right)$
Statement $II$ : In ventury tube shown $2 \mathrm{gh}=v_1^2-v_2^2$
In the light of the above statements, choose the most appropriate answer from the options given below.
Given below are two statements :
Statement $I$ : When speed of liquid is zero everywhere, pressure difference at any two points depends on equation $\mathrm{P}_1-\mathrm{P}_2=\rho \mathrm{g}\left(\mathrm{h}_2-\mathrm{h}_1\right)$
Statement $II$ : In ventury tube shown $2 \mathrm{gh}=v_1^2-v_2^2$
In the light of the above statements, choose the most appropriate answer from the options given below.
- [JEE MAIN 2024]
What type of fluid can be applied in Bernoulli’s equation ?
What type of fluid can be applied in Bernoulli’s equation ?
Bernoulli’s principle is based on the law of conservation of
Bernoulli’s principle is based on the law of conservation of
- [AIIMS 2001]
A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is $ r $ and angular velocity of rotation is $\omega $, then the difference in the heights of the liquid at the centre of the vessel and the edge is
A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is $ r $ and angular velocity of rotation is $\omega $, then the difference in the heights of the liquid at the centre of the vessel and the edge is
