આકૃતિના રેખાંકિત ભાગનું ક્ષેત્રફળ શોધો.
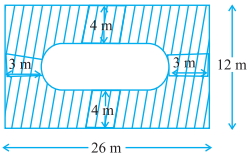
આકૃતિના રેખાંકિત ભાગનું ક્ષેત્રફળ શોધો.

join $GH$ and $FE$
Here, breadth of the rectangle $B C=12 \,m$
$\therefore$ Breadth of the inner rectangle $E F G H=12-(4+4)=4 \,cm$
which is equal to the diameter of the semi-circle $EJF,$ $d=4\,m$
$\therefore$ Radius of semi-circle $EJF,$ $r=2\, m$
$\therefore$ Length of inner rectangle $E F G H=26-(5+5)=16 \,m$
$\therefore$ Area of two semi-circles $E J F$ and $H I G=2\left(\frac{\pi r^{2}}{2}\right)=2 \times \pi \frac{(2)^{2}}{2}=4 \pi\, m$
Now, area of inner rectangle $E F G H=E H \times F G=16 \times 4=64\, m ^{2}$
and area of outer rectangle $A B C D=26 \times 12=312 \,m ^{2}$
$\therefore$ Area of shaded region $=$ Area of outer rectangle $-$ (Area of two semi-circles $+$ Area of inner rectangle)
$=312-(64+4 \pi)=(248-4 \pi) \,m ^{2}$

Similar Questions
એક વર્તુળના પરિઘનું માપ $88$ સેમી છે. તે વર્તુળને અંતર્ગત ચોરસની બાજુની લંબાઈ .......... સેમી હોય.
એક વર્તુળના પરિઘનું માપ $88$ સેમી છે. તે વર્તુળને અંતર્ગત ચોરસની બાજુની લંબાઈ .......... સેમી હોય.
વર્તુળની ત્રિજ્યા $7\,cm $ હોય તો લઘુવૃતાંશનું ક્ષેત્રફળ $\ldots \ldots \ldots \ldots cm ^{2}$ થાય.
વર્તુળની ત્રિજ્યા $7\,cm $ હોય તો લઘુવૃતાંશનું ક્ષેત્રફળ $\ldots \ldots \ldots \ldots cm ^{2}$ થાય.
એક ટ્રકના ટાયરનો પરિઘ $440\, cm $ છે અને તે પ્રતિ મિનિટ $250$ પરિભ્રમણ કરે છે. તો ટ્રકની ગતિ $\ldots \ldots \ldots \ldots km / h$ થાય.
એક ટ્રકના ટાયરનો પરિઘ $440\, cm $ છે અને તે પ્રતિ મિનિટ $250$ પરિભ્રમણ કરે છે. તો ટ્રકની ગતિ $\ldots \ldots \ldots \ldots km / h$ થાય.
આકૃતિમાં, $d$ વ્યાસવાળા વર્તુળને અંતર્ગત એક ચોરસ છે અને બીજો ચોરસ તે વર્તુળને બહિર્ગત છે. શું બહારના ચોરસનું ક્ષેત્રફળ, અંદરના ચોરસના ક્ષેત્રફળ કરતાં ચાર ગણું છે ? તમારા જવાબ માટે કારણ આપો.
આકૃતિમાં, $d$ વ્યાસવાળા વર્તુળને અંતર્ગત એક ચોરસ છે અને બીજો ચોરસ તે વર્તુળને બહિર્ગત છે. શું બહારના ચોરસનું ક્ષેત્રફળ, અંદરના ચોરસના ક્ષેત્રફળ કરતાં ચાર ગણું છે ? તમારા જવાબ માટે કારણ આપો.
આકૃતિમાં ચતુષ્કોણ $ABCD$ નાં શિરોબિંદુઓ $A, B, C$ અને $D$ ને કેન્દ્ર ગણી $21$ સેમીની ત્રિજ્યાનાં ચાપ દોરેલા છે. રેખાંકિત ભાગનું ક્ષેત્રફળ શોધો.(સેમી$^{2}$ માં)
આકૃતિમાં ચતુષ્કોણ $ABCD$ નાં શિરોબિંદુઓ $A, B, C$ અને $D$ ને કેન્દ્ર ગણી $21$ સેમીની ત્રિજ્યાનાં ચાપ દોરેલા છે. રેખાંકિત ભાગનું ક્ષેત્રફળ શોધો.(સેમી$^{2}$ માં)


