आकृति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
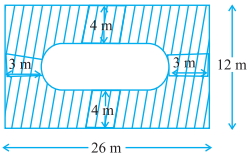
आकृति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

join $GH$ and $FE$
Here, breadth of the rectangle $B C=12 \,m$
$\therefore$ Breadth of the inner rectangle $E F G H=12-(4+4)=4 \,cm$
which is equal to the diameter of the semi-circle $EJF,$ $d=4\,m$
$\therefore$ Radius of semi-circle $EJF,$ $r=2\, m$
$\therefore$ Length of inner rectangle $E F G H=26-(5+5)=16 \,m$
$\therefore$ Area of two semi-circles $E J F$ and $H I G=2\left(\frac{\pi r^{2}}{2}\right)=2 \times \pi \frac{(2)^{2}}{2}=4 \pi\, m$
Now, area of inner rectangle $E F G H=E H \times F G=16 \times 4=64\, m ^{2}$
and area of outer rectangle $A B C D=26 \times 12=312 \,m ^{2}$
$\therefore$ Area of shaded region $=$ Area of outer rectangle $-$ (Area of two semi-circles $+$ Area of inner rectangle)
$=312-(64+4 \pi)=(248-4 \pi) \,m ^{2}$

Similar Questions
आकृति में, त्रिज्या $7.5 \,cm$ वाला एक वृत्त एक वर्ग के अंतर्गत खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए $(\pi=3.14$ लीजिए)।
आकृति में, त्रिज्या $7.5 \,cm$ वाला एक वृत्त एक वर्ग के अंतर्गत खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए $(\pi=3.14$ लीजिए)।
आकृति में, $14\, cm$ की त्रिज्याएँ लेकर तथा $P , Q$ और $R$ को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।( $cm ^{2}$ में )
आकृति में, $14\, cm$ की त्रिज्याएँ लेकर तथा $P , Q$ और $R$ को केंद्र मान कर चाप खींचे गये हैं। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।( $cm ^{2}$ में )
किसी ट्रैक्टर के अगले और पिछले पहियों के व्यास क्रमश: $80\, cm$ और $2\, m$ हैं। ज्ञात कीजिए कि पिछले पहिए द्वारा उतनी दूरी तय करने में कितने चक्कर लगाने होंगे, जितनी दूरी अगला पहिया $1400$ चक्कर लगाने पर तय करता है।
किसी ट्रैक्टर के अगले और पिछले पहियों के व्यास क्रमश: $80\, cm$ और $2\, m$ हैं। ज्ञात कीजिए कि पिछले पहिए द्वारा उतनी दूरी तय करने में कितने चक्कर लगाने होंगे, जितनी दूरी अगला पहिया $1400$ चक्कर लगाने पर तय करता है।
दो वृत्तों की परिधियाँ बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों के क्षेत्रफल भी बराबर हों? क्यों?
दो वृत्तों की परिधियाँ बराबर हैं। क्या यह आवश्यक है कि इन वृत्तों के क्षेत्रफल भी बराबर हों? क्यों?
आकृति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जहाँ $A , B , C$ और $D$ को केंद्र मान कर खींचे गये चाप युग्म में वर्ग $ABCD$ की क्रमश: $AB , BC , CD$ और $DA$ भुजाओं के मध्य-बिदुंंओ $P , Q , R$ और $S$ पर प्रतिच्छेद करते हैं $(\pi=3.14$ का प्रयोग कीजिए)। ($cm ^{2}$ में)
आकृति में, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, जहाँ $A , B , C$ और $D$ को केंद्र मान कर खींचे गये चाप युग्म में वर्ग $ABCD$ की क्रमश: $AB , BC , CD$ और $DA$ भुजाओं के मध्य-बिदुंंओ $P , Q , R$ और $S$ पर प्रतिच्छेद करते हैं $(\pi=3.14$ का प्रयोग कीजिए)। ($cm ^{2}$ में)


