Find the area of the shaded region in $Fig.$
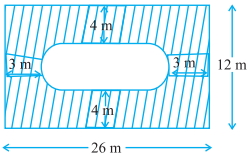
Find the area of the shaded region in $Fig.$

join $GH$ and $FE$
Here, breadth of the rectangle $B C=12 \,m$
$\therefore$ Breadth of the inner rectangle $E F G H=12-(4+4)=4 \,cm$
which is equal to the diameter of the semi-circle $EJF,$ $d=4\,m$
$\therefore$ Radius of semi-circle $EJF,$ $r=2\, m$
$\therefore$ Length of inner rectangle $E F G H=26-(5+5)=16 \,m$
$\therefore$ Area of two semi-circles $E J F$ and $H I G=2\left(\frac{\pi r^{2}}{2}\right)=2 \times \pi \frac{(2)^{2}}{2}=4 \pi\, m$
Now, area of inner rectangle $E F G H=E H \times F G=16 \times 4=64\, m ^{2}$
and area of outer rectangle $A B C D=26 \times 12=312 \,m ^{2}$
$\therefore$ Area of shaded region $=$ Area of outer rectangle $-$ (Area of two semi-circles $+$ Area of inner rectangle)
$=312-(64+4 \pi)=(248-4 \pi) \,m ^{2}$

Similar Questions
The central angles of two sectors of circles of radii $7 \,cm$ and $21\, cm$ are respectively $120^{\circ}$ and $40^{\circ}$. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
The central angles of two sectors of circles of radii $7 \,cm$ and $21\, cm$ are respectively $120^{\circ}$ and $40^{\circ}$. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Find the area of the shaded region in $Fig.$ where arcs drawn with centres $A , B , C$ and $D$ intersect in pairs at mid-points $P , Q , R$ and $S$ of the sides $AB , BC,$ $CD$ and $DA ,$ respectively of a square $ABCD$ (Use $\pi=3.14)$ (in $cm ^{2}$)
Find the area of the shaded region in $Fig.$ where arcs drawn with centres $A , B , C$ and $D$ intersect in pairs at mid-points $P , Q , R$ and $S$ of the sides $AB , BC,$ $CD$ and $DA ,$ respectively of a square $ABCD$ (Use $\pi=3.14)$ (in $cm ^{2}$)
The diameter of a circle with area $154\,cm ^{2}$ is $\ldots \ldots \ldots . cm$.
The diameter of a circle with area $154\,cm ^{2}$ is $\ldots \ldots \ldots . cm$.
The radius of a field in the shape of a sector is $50 \,m$. The cost of fencing its boundary is ₹ $5400$ at the rate of ₹ $30 / m$. Find the cost of tilling at the rate of ₹ $15 / m ^{2}$. (in ₹)
The radius of a field in the shape of a sector is $50 \,m$. The cost of fencing its boundary is ₹ $5400$ at the rate of ₹ $30 / m$. Find the cost of tilling at the rate of ₹ $15 / m ^{2}$. (in ₹)
Area of a circle is $5544 \,cm ^{2}$. Find its radius. (in $cm$)
Area of a circle is $5544 \,cm ^{2}$. Find its radius. (in $cm$)


