एक समान्तर प्लेट संधारित्र की धारिता $10\,\mu \,F$ (माइक्रो-फैराड) है, उसकी प्लेटों के मध्य में वायु भरी है। अब प्लेटों के बीच के आधे स्थान में एक परावैद्युत माध्यम, जिसका परावैद्युतांक $4$ है, भर दिया जााता है, जैसा कि चित्र में दिखाया गया है। संधारित्र की धारिता बदलकर .........$\mu \,F$ हो जाएगी
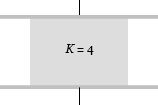
एक समान्तर प्लेट संधारित्र की धारिता $10\,\mu \,F$ (माइक्रो-फैराड) है, उसकी प्लेटों के मध्य में वायु भरी है। अब प्लेटों के बीच के आधे स्थान में एक परावैद्युत माध्यम, जिसका परावैद्युतांक $4$ है, भर दिया जााता है, जैसा कि चित्र में दिखाया गया है। संधारित्र की धारिता बदलकर .........$\mu \,F$ हो जाएगी

- A
$25$
- B
$20$
- C
$40$
- D
$5$
Similar Questions
दो एक समान आवेशित गोलों का समान लम्बाई की डोरियों से लटकाया गया है। डोरियाँ एक दूसरे से $37^{\circ}$ का कोण बनाती हैं। जब इन्हें $0.7$ ग्राम/सेमी. ${ }^3$, घनत्व के किसी द्रव में डुबाया जाता है, तो उनके बीच बना कोण वही रहता है। यदि गोले के पदार्थ का घनत्व $1.4$ग्राम/सेमी. ${ }^3$ हो, तो द्रव का परावैद्युतांक. . . . . . . . होगा। $\left(\tan 37^{\circ}=\frac{3}{4}\right)$.
दो एक समान आवेशित गोलों का समान लम्बाई की डोरियों से लटकाया गया है। डोरियाँ एक दूसरे से $37^{\circ}$ का कोण बनाती हैं। जब इन्हें $0.7$ ग्राम/सेमी. ${ }^3$, घनत्व के किसी द्रव में डुबाया जाता है, तो उनके बीच बना कोण वही रहता है। यदि गोले के पदार्थ का घनत्व $1.4$ग्राम/सेमी. ${ }^3$ हो, तो द्रव का परावैद्युतांक. . . . . . . . होगा। $\left(\tan 37^{\circ}=\frac{3}{4}\right)$.
- [JEE MAIN 2024]
समान्तर प्लेट संधारित्रों के एक संयोजन को एक निश्चित विभवान्तर पर रखा गया है। (चित्र देखिये)
जब $3\; mm$ मोटे गुटके को सभी संधारित्रों की प्लेटों के बीच डाला जाता है, तो वही विभवान्तर बनाये रखने के लिए प्लेटों के बीच की दूरी को $2.4\; mm$ से बढ़ाना पड़ता है। गुटके का परावैद्युतांक होगा
समान्तर प्लेट संधारित्रों के एक संयोजन को एक निश्चित विभवान्तर पर रखा गया है। (चित्र देखिये)
जब $3\; mm$ मोटे गुटके को सभी संधारित्रों की प्लेटों के बीच डाला जाता है, तो वही विभवान्तर बनाये रखने के लिए प्लेटों के बीच की दूरी को $2.4\; mm$ से बढ़ाना पड़ता है। गुटके का परावैद्युतांक होगा
- [JEE MAIN 2017]
एक समान्तर पट्ट संधारित्र जिसकी प्लेट का क्षेत्रफल $A$ तथा प्लेटो के बीच दूरी $d =2\,m$ है, की धारिता $4\,\mu\,F$ है। यदि उनके मध्य आधे स्थान को चित्रानुसार $K =3$ परावैधुतांक वाले परावैधुत पदार्थ से भर दिया जाये तो निकाय की नई धारिता $..........\mu\,F$ होगी।
एक समान्तर पट्ट संधारित्र जिसकी प्लेट का क्षेत्रफल $A$ तथा प्लेटो के बीच दूरी $d =2\,m$ है, की धारिता $4\,\mu\,F$ है। यदि उनके मध्य आधे स्थान को चित्रानुसार $K =3$ परावैधुतांक वाले परावैधुत पदार्थ से भर दिया जाये तो निकाय की नई धारिता $..........\mu\,F$ होगी।
- [JEE MAIN 2022]
दो वृत्तीय प्लेटों, जिनके बीच की दूरी $5 \,mm$ हैं, से एक समान्तर पट्टिका संधारित्र बनाया गया है जिसके बीच परावैध्युत स्थिरांक $2.2$ का एक परवैध्युत रखा गया है। जब परवैध्युत में विध्युत क्षेत्र $3 \times 10^{4} \,V / m$ है, तब धनात्मक प्लेट का आवेश घनत्व लगभग होगा:
दो वृत्तीय प्लेटों, जिनके बीच की दूरी $5 \,mm$ हैं, से एक समान्तर पट्टिका संधारित्र बनाया गया है जिसके बीच परावैध्युत स्थिरांक $2.2$ का एक परवैध्युत रखा गया है। जब परवैध्युत में विध्युत क्षेत्र $3 \times 10^{4} \,V / m$ है, तब धनात्मक प्लेट का आवेश घनत्व लगभग होगा:
- [JEE MAIN 2014]
किसी समान्तर पट्टिका संधारित्र व्यवस्था में संधारित्र की पट्टिका का क्षेत्रफल $2 \,m ^{2}$ तथा दो पट्टिकाओं के बीच पथकन् $1 \,m$ है। यदि पट्टिकाओं के बीच के रिक्त स्थान में $0.5\, m$ मोटाई तथा क्षेत्रफल $2 \,m ^{2}$ (आरेख देखिए) का कोई परावैधुत पदार्थ भर दें, तो इस व्यवस्था की धारिता $.....\,\varepsilon_{0}$ होगी। (पदार्थ का परावैधुतांक $=3.2$ ) (निकटतम पूर्णांक तक पूर्णांकित)
किसी समान्तर पट्टिका संधारित्र व्यवस्था में संधारित्र की पट्टिका का क्षेत्रफल $2 \,m ^{2}$ तथा दो पट्टिकाओं के बीच पथकन् $1 \,m$ है। यदि पट्टिकाओं के बीच के रिक्त स्थान में $0.5\, m$ मोटाई तथा क्षेत्रफल $2 \,m ^{2}$ (आरेख देखिए) का कोई परावैधुत पदार्थ भर दें, तो इस व्यवस्था की धारिता $.....\,\varepsilon_{0}$ होगी। (पदार्थ का परावैधुतांक $=3.2$ ) (निकटतम पूर्णांक तक पूर्णांकित)
- [JEE MAIN 2021]
