एक आवेश $Q$ एक $a$ भुजा वाले वर्गाकार सतह के केन्द्र से $a/2$ ऊँचाई पर रखा हुआ है (चित्र देखें)
वर्गाकार सतह से जाने वाला विघुत फ्लक्स होगा
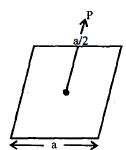
एक आवेश $Q$ एक $a$ भुजा वाले वर्गाकार सतह के केन्द्र से $a/2$ ऊँचाई पर रखा हुआ है (चित्र देखें)
वर्गाकार सतह से जाने वाला विघुत फ्लक्स होगा

- [JEE MAIN 2018]
- A
$\frac{Q}{{3{\varepsilon _0}}}$
- B
$\frac{Q}{{6{\varepsilon _0}}}$
- C
$\frac{Q}{{2{\varepsilon _0}}}$
- D
$\frac{Q}{{{\varepsilon _0}}}$
Similar Questions
धातु का एक अनावेशित गोला दो आवेशित प्लेटों के बीच चित्र के अनुसार रखा गया है वैद्युत बल रेखाओं की प्रकृति किस प्रकार की होगी
धातु का एक अनावेशित गोला दो आवेशित प्लेटों के बीच चित्र के अनुसार रखा गया है वैद्युत बल रेखाओं की प्रकृति किस प्रकार की होगी
चित्र में दिखाये गये बक्से से होकर विधुत क्षेत्र $\overrightarrow{ E }=4 xi -\left( y ^{2}+1\right) \hat{ j } N / C$ निकलता है। यदि बक्से के $ABCD$ तथा $BCGF$ समतलों में से होकर जाने वाले फ्लक्स का मान क्रमश: $\phi_{ I }$ तथा $\phi_{ II }$ है तब इनमें अन्तर $\left(\phi_{ I }-\phi_{ II }\right)$ $\left( Nm ^{2} / C \right)$ में होगा $......$
चित्र में दिखाये गये बक्से से होकर विधुत क्षेत्र $\overrightarrow{ E }=4 xi -\left( y ^{2}+1\right) \hat{ j } N / C$ निकलता है। यदि बक्से के $ABCD$ तथा $BCGF$ समतलों में से होकर जाने वाले फ्लक्स का मान क्रमश: $\phi_{ I }$ तथा $\phi_{ II }$ है तब इनमें अन्तर $\left(\phi_{ I }-\phi_{ II }\right)$ $\left( Nm ^{2} / C \right)$ में होगा $......$
- [JEE MAIN 2020]
चित्र में एक आवेशित पिण्ड से निकलने वाली वैद्युत बल रेखाएँ दिखाई गई हैं। यदि $A$ तथा $B$ पर वैद्युत क्षेत्र क्रमश: ${E_A}$ व ${E_B}$ हों तथा $A$ व $B$ के बीच की दूरी $r$ है तो
चित्र में एक आवेशित पिण्ड से निकलने वाली वैद्युत बल रेखाएँ दिखाई गई हैं। यदि $A$ तथा $B$ पर वैद्युत क्षेत्र क्रमश: ${E_A}$ व ${E_B}$ हों तथा $A$ व $B$ के बीच की दूरी $r$ है तो
- [AIIMS 2017]
प्रदर्शित चित्र में, $\mathrm{E}=2 \mathrm{x}^2 \hat{\mathrm{i}}-4 \mathrm{y} \hat{\mathrm{j}}+6 \hat{\mathrm{k}} \mathrm{N} / \mathrm{C}$ वैद्युत क्षेत्र में एक घनाभ स्थित है। घनाभ के अन्दर आवेश का परिणाम $\mathrm{n} \in_0 \mathrm{C}$ है। $\mathrm{n}$ का मान (यदि घनाभ की विमाएँ $1 \times 2 \times 3$ मी $^3$ है) हैं।
प्रदर्शित चित्र में, $\mathrm{E}=2 \mathrm{x}^2 \hat{\mathrm{i}}-4 \mathrm{y} \hat{\mathrm{j}}+6 \hat{\mathrm{k}} \mathrm{N} / \mathrm{C}$ वैद्युत क्षेत्र में एक घनाभ स्थित है। घनाभ के अन्दर आवेश का परिणाम $\mathrm{n} \in_0 \mathrm{C}$ है। $\mathrm{n}$ का मान (यदि घनाभ की विमाएँ $1 \times 2 \times 3$ मी $^3$ है) हैं।
- [JEE MAIN 2023]
$2.4 \,m$ व्यास के किसी एकसमान आवेशित चालक गोले का पृष्ठीय आवेश छनत्व $80.0 \mu C / m ^{2}$ है।
$(a)$ गोले पर आवेश ज्ञात कीजिए।
$(b)$ गोले के पृष्ठ से निर्गत कुल वैद्युत फ्लक्स क्या है?
$2.4 \,m$ व्यास के किसी एकसमान आवेशित चालक गोले का पृष्ठीय आवेश छनत्व $80.0 \mu C / m ^{2}$ है।
$(a)$ गोले पर आवेश ज्ञात कीजिए।
$(b)$ गोले के पृष्ठ से निर्गत कुल वैद्युत फ्लक्स क्या है?
