A charge $Q$ is placed at a distance $a/2$ above the centre of the square surface of edge $a$ as shown in the figure. The electric flux through the square surface is
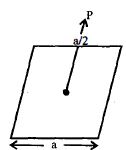
A charge $Q$ is placed at a distance $a/2$ above the centre of the square surface of edge $a$ as shown in the figure. The electric flux through the square surface is

- [JEE MAIN 2018]
- A
$\frac{Q}{{3{\varepsilon _0}}}$
- B
$\frac{Q}{{6{\varepsilon _0}}}$
- C
$\frac{Q}{{2{\varepsilon _0}}}$
- D
$\frac{Q}{{{\varepsilon _0}}}$
Similar Questions
A few electric field lines for a system of two charges $Q_1$ and $Q_2$ fixed at two different points on the $x$ -axis are shown in the figure. These lines suggest that:-
A few electric field lines for a system of two charges $Q_1$ and $Q_2$ fixed at two different points on the $x$ -axis are shown in the figure. These lines suggest that:-
How field lines depend on area or on solid angle made by area ?
How field lines depend on area or on solid angle made by area ?
An electric field converges at the origin whose magnitude is given by the expression $E = 100\,r\,Nt/Coul$, where $r$ is the distance measured from the origin.
An electric field converges at the origin whose magnitude is given by the expression $E = 100\,r\,Nt/Coul$, where $r$ is the distance measured from the origin.
Shown below is a distribution of charges. The flux of electric field due to these charges through the surface $S$ is
Shown below is a distribution of charges. The flux of electric field due to these charges through the surface $S$ is
- [AIIMS 2003]
Why do electric field lines not form closed loop ?
Why do electric field lines not form closed loop ?
