आपने सरकस में 'मौत के कुएँ' ( एक खोखला जालयुक्त गोलीय चैम्बर ताकि उसके भीतर के क्रियाकलापों को दर्शक देख सकें) में मोटरसाइकिल सवार को ऊर्ध्वाधर लूप में मोटरसाइकिल चलाते हुए देखा होगा। स्पष्ट कीजिए कि वह मोटरसाइकिल सवार नीचे से कोई सहारा न होने पर भी गोले के उच्चतम बिंदु से नीचे क्यों नहीं गिरता? यदि चैम्बर की त्रिज्या $25\, m$ है, तो ऊर्ध्वाधर लूप को पूरा करने के लिए मोटरसाइकिल की न्यूनतम चाल कितनी होनी चाहिए ?
आपने सरकस में 'मौत के कुएँ' ( एक खोखला जालयुक्त गोलीय चैम्बर ताकि उसके भीतर के क्रियाकलापों को दर्शक देख सकें) में मोटरसाइकिल सवार को ऊर्ध्वाधर लूप में मोटरसाइकिल चलाते हुए देखा होगा। स्पष्ट कीजिए कि वह मोटरसाइकिल सवार नीचे से कोई सहारा न होने पर भी गोले के उच्चतम बिंदु से नीचे क्यों नहीं गिरता? यदि चैम्बर की त्रिज्या $25\, m$ है, तो ऊर्ध्वाधर लूप को पूरा करने के लिए मोटरसाइकिल की न्यूनतम चाल कितनी होनी चाहिए ?
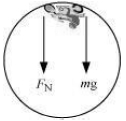
In a death-well, a motorcyclist does not fall at the top point of a vertical loop because both the force of normal reaction and the weight of the motorcyclist act downward and are balanced by the centripetal force. This situation is shown in the following figure.
The net force acting on the motorcyclist is the sum of the normal force $(F_N)$ and the force due to gravity $(F_g = mg).$
The equation of motion for the centripetal acceleration $a_{c},$ can be written as:
$F_{\text {net }}=m a c$
$F_{ N }+F_{ r }=m a_{ e }$
$F_{ N }+m g=\frac{m v^{2}}{r}$
Normal reaction is provided by the speed of the motorcyclist. At the minimum speed $\left(v_{\min }\right), F_{ N }=0$
$m g=\frac{m v_{\min }^{2}}{r}$
$\therefore v_{\min } =\sqrt{r g}$ $=\sqrt{25 \times 10}=15.8\, m / s$
Similar Questions
$200\, g$ द्रव्यमान का कोई ब्लॉक किसी नियत चाल से एक क्षैतिज वत्ताकार खाँचे में जिसकी ऊर्ध्वाधर पार्श्व दीवारों की त्रिज्या $20 \,cm$ है, पर गति करता है। यदि ब्लॉक एक चक्कर पूरा करने में $40 \,s$ लेता है, तो खाँचे की पार्श्व दीवारों द्वारा आरोपित अभिलम्बवत् बल का मान होगा
$200\, g$ द्रव्यमान का कोई ब्लॉक किसी नियत चाल से एक क्षैतिज वत्ताकार खाँचे में जिसकी ऊर्ध्वाधर पार्श्व दीवारों की त्रिज्या $20 \,cm$ है, पर गति करता है। यदि ब्लॉक एक चक्कर पूरा करने में $40 \,s$ लेता है, तो खाँचे की पार्श्व दीवारों द्वारा आरोपित अभिलम्बवत् बल का मान होगा
- [JEE MAIN 2021]
एक कार उच्च गति से जब एक मोड़ पर मुड़ती है, तो इस पर बाहर की ओर एक बल कार्य करता है। इसका कारण है
एक कार उच्च गति से जब एक मोड़ पर मुड़ती है, तो इस पर बाहर की ओर एक बल कार्य करता है। इसका कारण है
एक समतल सड़क के वक्र की त्रिज्या $75\,m$ है। इस वक्रीय सड़क पर कार की बिना फिसले अधिकतम चाल $30\,m / s$ हो सकती है। यदि वक्रीय सड़क की त्रिज्या को $48\,m$ तक परिवर्तित किया जाता है तथा सड़क व टायर के बीच घर्पण गुणांक समान रहता है, तब अधिकतम अनुमत चाल $m / s$ में ज्ञात कीजिए।
एक समतल सड़क के वक्र की त्रिज्या $75\,m$ है। इस वक्रीय सड़क पर कार की बिना फिसले अधिकतम चाल $30\,m / s$ हो सकती है। यदि वक्रीय सड़क की त्रिज्या को $48\,m$ तक परिवर्तित किया जाता है तथा सड़क व टायर के बीच घर्पण गुणांक समान रहता है, तब अधिकतम अनुमत चाल $m / s$ में ज्ञात कीजिए।
- [JEE MAIN 2022]
एक समतल सड़क पर $4.9$ मीटर/सैकण्ड की चाल से गतिमान साइकिल सवार $4$ मीटर त्रिज्या के तीक्ष्ण वृत्ताकार मोड़ पर मुड़ सकता है। तब साइकिल के टायरों तथा सड़क के बीच घर्षण गुणांक है
एक समतल सड़क पर $4.9$ मीटर/सैकण्ड की चाल से गतिमान साइकिल सवार $4$ मीटर त्रिज्या के तीक्ष्ण वृत्ताकार मोड़ पर मुड़ सकता है। तब साइकिल के टायरों तथा सड़क के बीच घर्षण गुणांक है
- [AIIMS 1999]
$1000 $ मीटर त्रिज्या का वृत्ताकार मार्ग जिसका क्षैतिज से कोण $45°$ है, इस पर एक $2000$ किग्रा की कार मुड़ रही है। इस कार हेतु अधिकतम सुरक्षित चाल ....... $m/s$ होगी यदि सड़क तथा टायरों के मध्य घर्षण गुणांक $0.5$ है
$1000 $ मीटर त्रिज्या का वृत्ताकार मार्ग जिसका क्षैतिज से कोण $45°$ है, इस पर एक $2000$ किग्रा की कार मुड़ रही है। इस कार हेतु अधिकतम सुरक्षित चाल ....... $m/s$ होगी यदि सड़क तथा टायरों के मध्य घर्षण गुणांक $0.5$ है


