एक $R$ त्रिज्या के गोले में समान घनत्व $\rho$ का आवेश वितरित है। यदि इस गोले से $\frac{ R }{2}$ त्रिज्या का एक गोला काटकर चित्रानुसार निकाल दिया जाय तो बचे हुए भाग के कारण बिन्दु ओं $A$ तथा $B$ पर विधुत क्षेत्र (क्रमशः $\overrightarrow{ E }_{ A }$ तथा $\overrightarrow{ E }_{ B }$ ) के मान का अनुपात $\frac{\left|\overrightarrow{ E }_{ A }\right|}{\left|\overrightarrow{ E }_{ B }\right|}$ होगा।
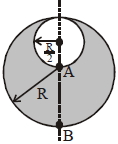
एक $R$ त्रिज्या के गोले में समान घनत्व $\rho$ का आवेश वितरित है। यदि इस गोले से $\frac{ R }{2}$ त्रिज्या का एक गोला काटकर चित्रानुसार निकाल दिया जाय तो बचे हुए भाग के कारण बिन्दु ओं $A$ तथा $B$ पर विधुत क्षेत्र (क्रमशः $\overrightarrow{ E }_{ A }$ तथा $\overrightarrow{ E }_{ B }$ ) के मान का अनुपात $\frac{\left|\overrightarrow{ E }_{ A }\right|}{\left|\overrightarrow{ E }_{ B }\right|}$ होगा।

- [JEE MAIN 2020]
- A
$\frac{18}{54}$
- B
$\frac{21}{34}$
- C
$\frac{17}{54}$
- D
$\frac{18}{34}$
Similar Questions
चित्र में दर्शाये अनुसार तीन अनन्त लम्बाई की आवेशित चादरें रखी है। बिन्दु $P$ पर विद्युत क्षेत्र होगा
चित्र में दर्शाये अनुसार तीन अनन्त लम्बाई की आवेशित चादरें रखी है। बिन्दु $P$ पर विद्युत क्षेत्र होगा
- [IIT 2005]
एक चालक गोले की त्रिज्या $R = 20$ सेमी. है। इसे $Q = 16\,\mu C$ आवेश दिया गया। इसके केन्द्र पर तीव्रता $\overrightarrow E $ है
एक चालक गोले की त्रिज्या $R = 20$ सेमी. है। इसे $Q = 16\,\mu C$ आवेश दिया गया। इसके केन्द्र पर तीव्रता $\overrightarrow E $ है
$12\, cm$ त्रिज्या वाले एक गोलीय चालक के पृष्ठ पर $1.6 \times 10^{-7} \,C$ का आवेश एकसमान रूप से वितरित है।
$(a)$ गोले के अंदर
$(b)$ गोले के ठीक बाहर
$(c)$ गोले के केंद्र से $18 cm$ पर अवस्थित, किसी बिंदु पर विध्यूत क्षेत्र क्या होगा?
$12\, cm$ त्रिज्या वाले एक गोलीय चालक के पृष्ठ पर $1.6 \times 10^{-7} \,C$ का आवेश एकसमान रूप से वितरित है।
$(a)$ गोले के अंदर
$(b)$ गोले के ठीक बाहर
$(c)$ गोले के केंद्र से $18 cm$ पर अवस्थित, किसी बिंदु पर विध्यूत क्षेत्र क्या होगा?
वैद्युत क्षेत्र ${r^o}$ के साथ परिवर्तित होता है
वैद्युत क्षेत्र ${r^o}$ के साथ परिवर्तित होता है
एक बिन्दु आवेश $Q$, एक एकसमान रेखीय आवेश घनत्व (Linear charge density) $\lambda$ वाले अनन्त लम्बाई तके तार तथा एक एकसमान पृष्ठ आवेश घनत्व (uniform surface charge density) $\sigma$ वाले अनन्त समतल चादर के कारण $r$ दूरी पर विद्युत क्षेत्र की तीव्रतायें क्रमश: $E_1(r), E_2(r)$ तथा $E_3(r)$ हैं यदि एक दी गई दूरी $r_0$ पर $E_1\left(r_0\right)=E_2\left(r_0\right)=E_3\left(r_0\right)$ तब
एक बिन्दु आवेश $Q$, एक एकसमान रेखीय आवेश घनत्व (Linear charge density) $\lambda$ वाले अनन्त लम्बाई तके तार तथा एक एकसमान पृष्ठ आवेश घनत्व (uniform surface charge density) $\sigma$ वाले अनन्त समतल चादर के कारण $r$ दूरी पर विद्युत क्षेत्र की तीव्रतायें क्रमश: $E_1(r), E_2(r)$ तथा $E_3(r)$ हैं यदि एक दी गई दूरी $r_0$ पर $E_1\left(r_0\right)=E_2\left(r_0\right)=E_3\left(r_0\right)$ तब
- [IIT 2014]
