$\mathrm{R}$ ત્રિજ્યા ધરાવતા ગોળા પર વિજભારઘનતા $\rho$ છે.જો તેમાથી $\frac{\mathrm{R}}{2}$ ત્રિજ્યા ધરાવતો ભાગ કાપી નાખવામાં આવે તો $\frac{\left|\overrightarrow{\mathrm{E}}_{\mathrm{A}}\right|}{\left|\overrightarrow{\mathrm{E}}_{\mathrm{B}}\right|}$ નો ગુણોત્તર કેટલો થાય? જ્યાં $\overrightarrow{\mathrm{E}}_{\mathrm{A}}$ અને $\overrightarrow{\mathrm{E}}_{\mathrm{B}}$ બિંદુ $\mathrm{A}$ અને બિંદુ $\mathrm{B}$ પાસે વિદ્યુતક્ષેત્ર છે.
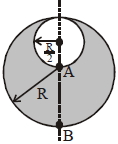
$\mathrm{R}$ ત્રિજ્યા ધરાવતા ગોળા પર વિજભારઘનતા $\rho$ છે.જો તેમાથી $\frac{\mathrm{R}}{2}$ ત્રિજ્યા ધરાવતો ભાગ કાપી નાખવામાં આવે તો $\frac{\left|\overrightarrow{\mathrm{E}}_{\mathrm{A}}\right|}{\left|\overrightarrow{\mathrm{E}}_{\mathrm{B}}\right|}$ નો ગુણોત્તર કેટલો થાય? જ્યાં $\overrightarrow{\mathrm{E}}_{\mathrm{A}}$ અને $\overrightarrow{\mathrm{E}}_{\mathrm{B}}$ બિંદુ $\mathrm{A}$ અને બિંદુ $\mathrm{B}$ પાસે વિદ્યુતક્ષેત્ર છે.
- [JEE MAIN 2020]
- A
$\frac{18}{54}$
- B
$\frac{21}{34}$
- C
$\frac{17}{54}$
- D
$\frac{18}{34}$
Similar Questions
પરમાણુ માટેના પ્રારંભિક મોડેલમાં, $Ze$ વિદ્યુતભાર ધરાવતું ધન વિધુતભારિત બિંદુવતુ ન્યુક્લિયસ તેની આસપાસ $R$ ત્રિજ્યા સુધી નિયમિત ઘનતાના ઋણ વિધુતભાર વડે ઘેરાયેલું છે. સમગ્રપણે પરમાણુ તટસ્થ છે. આ મૉડેલ માટે ન્યુક્લિયસથી $r$ અંતરે વિધુતક્ષેત્ર કેટલું હશે ?
પરમાણુ માટેના પ્રારંભિક મોડેલમાં, $Ze$ વિદ્યુતભાર ધરાવતું ધન વિધુતભારિત બિંદુવતુ ન્યુક્લિયસ તેની આસપાસ $R$ ત્રિજ્યા સુધી નિયમિત ઘનતાના ઋણ વિધુતભાર વડે ઘેરાયેલું છે. સમગ્રપણે પરમાણુ તટસ્થ છે. આ મૉડેલ માટે ન્યુક્લિયસથી $r$ અંતરે વિધુતક્ષેત્ર કેટલું હશે ?
આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરો
આકૃતિમાં એક ખૂબ મોટું ધન વિદ્યુતભારિત સમતલ પૃષ્ઠ દર્શાવેલ છે. $P _{1}$ અને $P _{2}$ એ વિદ્યુતભાર વિતરણથી $l$ અને $2 l$ જેટલા લઘુત્તમ અંતરે બે બિંદુુઓ છે. જે પૃષ્ઠ વીજભાર ઘનતા $\sigma$ હોય, તો $P_{1}$ અને $P_{2}$ આગળ વિદ્યુતક્ષેત્ર $E_{1}$ અને $E_{2}$ માટે સાચો વિકલ્પ પસંદ કરો
- [JEE MAIN 2022]
વિધુતભારિત ગોળાની બહારના વિસ્તારમાં ગાઉસના પ્રમેય પરથી વિધુતક્ષેત્રનું સૂત્ર મેળવો.
વિધુતભારિત ગોળાની બહારના વિસ્તારમાં ગાઉસના પ્રમેય પરથી વિધુતક્ષેત્રનું સૂત્ર મેળવો.
$R$ ત્રિજયા ધરાવતા વિદ્યુતભારીત વાહક ગોળીય કવચના કેન્દ્રથી $\frac{{3R}}{2}$ અંતરે વિદ્યુતક્ષેત્ર $E\; V/m$ છે. તેના કેન્દ્રથી $\frac{R}{2}$ અંતરે વિદ્યુતક્ષેત્ર કેટલું થાય?
$R$ ત્રિજયા ધરાવતા વિદ્યુતભારીત વાહક ગોળીય કવચના કેન્દ્રથી $\frac{{3R}}{2}$ અંતરે વિદ્યુતક્ષેત્ર $E\; V/m$ છે. તેના કેન્દ્રથી $\frac{R}{2}$ અંતરે વિદ્યુતક્ષેત્ર કેટલું થાય?
- [AIPMT 2010]
બે મોટી, પાતળી ધાતુની પ્લેટો એકબીજાની નજીક અને સમાંતર છે. તેમની અંદરની બાજુઓ પર વિરૂદ્ધ ચિહ્નો ધરાવતી અને $17.0\times 10^{-22}\; C/m^2$ મૂલ્યની વિદ્યુતભારની પૃષ્ઠઘનતા છે. $(a)$ પ્રથમ પ્લેટની બહારના વિસ્તારમાં $(b)$ બીજી પ્લેટની બહારના વિસ્તારમાં અને $(c)$ બંને પ્લેટોની વચ્ચેના વિસ્તારમાં વિદ્યુતક્ષેત્ર $E$ શોધો.
બે મોટી, પાતળી ધાતુની પ્લેટો એકબીજાની નજીક અને સમાંતર છે. તેમની અંદરની બાજુઓ પર વિરૂદ્ધ ચિહ્નો ધરાવતી અને $17.0\times 10^{-22}\; C/m^2$ મૂલ્યની વિદ્યુતભારની પૃષ્ઠઘનતા છે. $(a)$ પ્રથમ પ્લેટની બહારના વિસ્તારમાં $(b)$ બીજી પ્લેટની બહારના વિસ્તારમાં અને $(c)$ બંને પ્લેટોની વચ્ચેના વિસ્તારમાં વિદ્યુતક્ષેત્ર $E$ શોધો.