चित्र में दर्शाए अनुसार $10 \,cm$ भुजा के किसी वर्ग के केंद्र से ठीक $5\, cm$ ऊँचाई पर कोई $+10 \mu C$ आवेश रखा है। इस वर्ग से गुजरने वाले वैध्यूत फ्लक्स का परिमाण क्या है? (संकेत : वर्ग को $10 \,cm$ किनारे के किसी घन का एक फलक मानिए।)
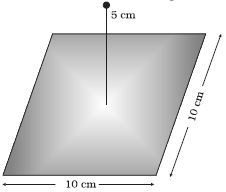
चित्र में दर्शाए अनुसार $10 \,cm$ भुजा के किसी वर्ग के केंद्र से ठीक $5\, cm$ ऊँचाई पर कोई $+10 \mu C$ आवेश रखा है। इस वर्ग से गुजरने वाले वैध्यूत फ्लक्स का परिमाण क्या है? (संकेत : वर्ग को $10 \,cm$ किनारे के किसी घन का एक फलक मानिए।)

The square can be considered as one face of a cube of edge $10 \,cm$ with a centre where charge $q$ is placed. According to Gauss's theorem for a cube, total electric flux is through all its six faces.
$\phi_{\text {Total}}=\frac{q}{\varepsilon_{0}}$
Hence, electric flux through one face of the cube i.e., through the square is
$\phi=\frac{\phi_{\text {Total}}}{6}=\frac{1}{6} \cdot \frac{q}{\varepsilon_{0}}$
Where, $\varepsilon_{0}=$ Permittivity of free space $=8.854 \times 10^{-12}\, N ^{-1} \,C ^{2} \,m ^{-2}$
$q=10\, \mu \,C=10 \times 10^{-6} \,C$
$=1.88 \times 10^{5} \,N \,m ^{2} \,C ^{-1}$
$\therefore \phi=\frac{1}{6} \cdot \frac{10 \times 10^{-6}}{8.854 \times 10^{-12}}$
Therefore, electric flux through the square is $1.88 \times 10^{5} \;N \;m ^{2} \,C ^{-1}$
Similar Questions
असत्य कथन छाँटिए :
$(a)$ गौसीय सतह में प्रवेश करने वाली विधुत बल रेखाएं ऋणात्मक फ्लक्स प्रदान करती है।
$(b)$ एक आवेश $'q'$ एक घन के केन्द्र पर रखा है। सभी फलको से निर्गत फ्लक्स समान होगा।
$(c)$ एक समान विधुत क्षेत्र में कोई आवेश न रखने वाली बन्द गौसीय सतह से निर्गत परिणामी फ्लक्स शून्य होता है।
$(d)$ जब विधुत क्षेत्र गौसीय सतह के समान्तर होती है, तो यह परिमित अशून्य फ्लक्स प्रदान करती है।
नीचे दिए गये विकल्पों में उपयुक्त उत्तर चुनिए :
असत्य कथन छाँटिए :
$(a)$ गौसीय सतह में प्रवेश करने वाली विधुत बल रेखाएं ऋणात्मक फ्लक्स प्रदान करती है।
$(b)$ एक आवेश $'q'$ एक घन के केन्द्र पर रखा है। सभी फलको से निर्गत फ्लक्स समान होगा।
$(c)$ एक समान विधुत क्षेत्र में कोई आवेश न रखने वाली बन्द गौसीय सतह से निर्गत परिणामी फ्लक्स शून्य होता है।
$(d)$ जब विधुत क्षेत्र गौसीय सतह के समान्तर होती है, तो यह परिमित अशून्य फ्लक्स प्रदान करती है।
नीचे दिए गये विकल्पों में उपयुक्त उत्तर चुनिए :
- [JEE MAIN 2021]
एक धातु के गोले को दो विपरीत आवेशित पद्वियों के बीच में रखा जाता है. रेखा-क्षेत्रों का सही चित्रण निम्न में से किस चित्र में प्रदर्शित है?
एक धातु के गोले को दो विपरीत आवेशित पद्वियों के बीच में रखा जाता है. रेखा-क्षेत्रों का सही चित्रण निम्न में से किस चित्र में प्रदर्शित है?
- [KVPY 2016]
निम्न चित्र में आवेश वितरण प्रदर्शित है। इन आवेशों के कारण पृष्ठ $S$ से गुजरने वाला विद्युत फ्लक्स है
निम्न चित्र में आवेश वितरण प्रदर्शित है। इन आवेशों के कारण पृष्ठ $S$ से गुजरने वाला विद्युत फ्लक्स है
- [AIIMS 2003]
एक धात्विक घन को धनावेश $Q$ दिया गया है। इस व्यवस्था के लिए, निम्न में से कौनसा कथन सत्य है
एक धात्विक घन को धनावेश $Q$ दिया गया है। इस व्यवस्था के लिए, निम्न में से कौनसा कथन सत्य है
$2 \mathrm{~L} \times 2 \mathrm{~L} \times \mathrm{L}$ विमा वाले एक घनाभ के पृष्ठ ' $\mathrm{S}$ ' जिसका क्षेत्रफल $4 \mathrm{~L}^2$ हैं, के केन्द्र पर $q$ आवेश रखा है। ' $\mathrm{S}$ ' के विपरीत पृष्ठ से गुजरने वाला फ्लक्स है:
$2 \mathrm{~L} \times 2 \mathrm{~L} \times \mathrm{L}$ विमा वाले एक घनाभ के पृष्ठ ' $\mathrm{S}$ ' जिसका क्षेत्रफल $4 \mathrm{~L}^2$ हैं, के केन्द्र पर $q$ आवेश रखा है। ' $\mathrm{S}$ ' के विपरीत पृष्ठ से गुजरने वाला फ्लक्स है:
- [JEE MAIN 2023]


