A point charge $+10\; \mu \,C$ is a distance $5 cm$ directly above the centre of a square of side $10 \;cm ,$ as shown in Figure. What is the magnitude of the electric flux through the square?
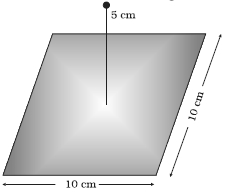
A point charge $+10\; \mu \,C$ is a distance $5 cm$ directly above the centre of a square of side $10 \;cm ,$ as shown in Figure. What is the magnitude of the electric flux through the square?
The square can be considered as one face of a cube of edge $10 \,cm$ with a centre where charge $q$ is placed. According to Gauss's theorem for a cube, total electric flux is through all its six faces.
$\phi_{\text {Total}}=\frac{q}{\varepsilon_{0}}$
Hence, electric flux through one face of the cube i.e., through the square is
$\phi=\frac{\phi_{\text {Total}}}{6}=\frac{1}{6} \cdot \frac{q}{\varepsilon_{0}}$
Where, $\varepsilon_{0}=$ Permittivity of free space $=8.854 \times 10^{-12}\, N ^{-1} \,C ^{2} \,m ^{-2}$
$q=10\, \mu \,C=10 \times 10^{-6} \,C$
$=1.88 \times 10^{5} \,N \,m ^{2} \,C ^{-1}$
$\therefore \phi=\frac{1}{6} \cdot \frac{10 \times 10^{-6}}{8.854 \times 10^{-12}}$
Therefore, electric flux through the square is $1.88 \times 10^{5} \;N \;m ^{2} \,C ^{-1}$
Similar Questions
Draw electric field lines when two positive charges are near.
Draw electric field lines when two positive charges are near.
An electric line of force in the $xy$ plane is given by equation ${x^2} + {y^2} = 1$. A particle with unit positive charge, initially at rest at the point $x = 1,\;y = 0$ in the $xy$ plane
An electric line of force in the $xy$ plane is given by equation ${x^2} + {y^2} = 1$. A particle with unit positive charge, initially at rest at the point $x = 1,\;y = 0$ in the $xy$ plane
- [IIT 1988]
Assertion : Four point charges $q_1,$ $q_2$, $q_3$ and $q_4$ are as shown in figure. The flux over the shown Gaussian surface depends only on charges $q_1$ and $q_2$.
Reason : Electric field at all points on Gaussian surface depends only on charges $q_1$ and $q_2$ .
Assertion : Four point charges $q_1,$ $q_2$, $q_3$ and $q_4$ are as shown in figure. The flux over the shown Gaussian surface depends only on charges $q_1$ and $q_2$.
Reason : Electric field at all points on Gaussian surface depends only on charges $q_1$ and $q_2$ .
- [AIIMS 2012]
In figure $+Q$ charge is located at one of the edge of the cube, then electric flux through cube due to $+Q$ charge is
In figure $+Q$ charge is located at one of the edge of the cube, then electric flux through cube due to $+Q$ charge is
The electric flux passing through the cube for the given arrangement of charges placed at the corners of the cube (as shown in the figure) is
The electric flux passing through the cube for the given arrangement of charges placed at the corners of the cube (as shown in the figure) is