આકૃતિ માં દર્શાવ્યા મુજબ $10 \,cm$ બાજુવાળા એક ચોરસના કેન્દ્રથી બરાબર ઉપર $5 \,cm$ અંતરે $+10\; \mu\, C$ બિંદુવતુ વિદ્યુતભાર રહેલો છે. ચોરસમાંથી વિદ્યુત ફલક્સનું મૂલ્ય કેટલું હશે? (સૂચન ચોરસને $10\, cm$ ની ધારવાળા ઘનની એક બાજુ તરીકે વિચારો.)
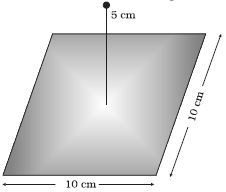
આકૃતિ માં દર્શાવ્યા મુજબ $10 \,cm$ બાજુવાળા એક ચોરસના કેન્દ્રથી બરાબર ઉપર $5 \,cm$ અંતરે $+10\; \mu\, C$ બિંદુવતુ વિદ્યુતભાર રહેલો છે. ચોરસમાંથી વિદ્યુત ફલક્સનું મૂલ્ય કેટલું હશે? (સૂચન ચોરસને $10\, cm$ ની ધારવાળા ઘનની એક બાજુ તરીકે વિચારો.)
The square can be considered as one face of a cube of edge $10 \,cm$ with a centre where charge $q$ is placed. According to Gauss's theorem for a cube, total electric flux is through all its six faces.
$\phi_{\text {Total}}=\frac{q}{\varepsilon_{0}}$
Hence, electric flux through one face of the cube i.e., through the square is
$\phi=\frac{\phi_{\text {Total}}}{6}=\frac{1}{6} \cdot \frac{q}{\varepsilon_{0}}$
Where, $\varepsilon_{0}=$ Permittivity of free space $=8.854 \times 10^{-12}\, N ^{-1} \,C ^{2} \,m ^{-2}$
$q=10\, \mu \,C=10 \times 10^{-6} \,C$
$=1.88 \times 10^{5} \,N \,m ^{2} \,C ^{-1}$
$\therefore \phi=\frac{1}{6} \cdot \frac{10 \times 10^{-6}}{8.854 \times 10^{-12}}$
Therefore, electric flux through the square is $1.88 \times 10^{5} \;N \;m ^{2} \,C ^{-1}$
Similar Questions
એક વિસ્તારમાં વિદ્યુતક્ષેત્ર એકરૂપ છે. અને $\vec{E}=a \hat{i}+b \hat{j}+c \hat{k}$ વડે આપવામાં આવેલ છે. $\vec{A}=\pi R^2 \hat{i}$ ક્ષેત્રફળની સપાટી સાથે સંકળાયેલ વિદ્યુત ફલક્સ કેટલું છે?
એક વિસ્તારમાં વિદ્યુતક્ષેત્ર એકરૂપ છે. અને $\vec{E}=a \hat{i}+b \hat{j}+c \hat{k}$ વડે આપવામાં આવેલ છે. $\vec{A}=\pi R^2 \hat{i}$ ક્ષેત્રફળની સપાટી સાથે સંકળાયેલ વિદ્યુત ફલક્સ કેટલું છે?
નીચે બે વિધાનો આપેલા છે એકને કથન $A$ તરીકે અને બીજાને કારણ $R$ તરીકે લેબલ કરવામાં આવે છે.
કથન $A$: $30 \times 10^{-5}\,Cm$ દ્વિધ્રુવીની ચાકમાત્રા ધરાવતા વિદ્યુત દ્વિધ્રુવીને બંંધ સપાટીમાં આવરતા તેમાંથી બહાર આવતું ચોખ્ખુ ફલકસ શૂન્ય હોય.
કરણ $R$: વિદ્યુત દ્રીધ્રુવી બે સમાન અને વિરુદ્ધ વીજભાર ધરાવે છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પો માંથી સાચો જવાબ પસંદ કરો.
નીચે બે વિધાનો આપેલા છે એકને કથન $A$ તરીકે અને બીજાને કારણ $R$ તરીકે લેબલ કરવામાં આવે છે.
કથન $A$: $30 \times 10^{-5}\,Cm$ દ્વિધ્રુવીની ચાકમાત્રા ધરાવતા વિદ્યુત દ્વિધ્રુવીને બંંધ સપાટીમાં આવરતા તેમાંથી બહાર આવતું ચોખ્ખુ ફલકસ શૂન્ય હોય.
કરણ $R$: વિદ્યુત દ્રીધ્રુવી બે સમાન અને વિરુદ્ધ વીજભાર ધરાવે છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પો માંથી સાચો જવાબ પસંદ કરો.
- [JEE MAIN 2023]
સાદા વિધુતભાર વિતરણની ક્ષેત્રરેખાઓ દોરો.
સાદા વિધુતભાર વિતરણની ક્ષેત્રરેખાઓ દોરો.
વિદ્યુતક્ષેત્રમાં બે ગાઉસિયન ઘન આકૃતિમાં દર્શાવેલ છે. તીર અને મૂલ્ય એ વિદ્યુતક્ષેત્રની દિશા અને મૂલ્ય ($N-m^2/C$) દર્શાવે છે. તો ઘનમા રહેલો કુલ વિદ્યુતભાર કેટલો હશે?
વિદ્યુતક્ષેત્રમાં બે ગાઉસિયન ઘન આકૃતિમાં દર્શાવેલ છે. તીર અને મૂલ્ય એ વિદ્યુતક્ષેત્રની દિશા અને મૂલ્ય ($N-m^2/C$) દર્શાવે છે. તો ઘનમા રહેલો કુલ વિદ્યુતભાર કેટલો હશે?
- [AIIMS 2011]
ડાઇપોલને ઘેરતી યાઈચ્છિક સપાટી વિચારો તો સપાટીમાંથી પસાર થતું ફલક્સ કેટલું હશે ?
ડાઇપોલને ઘેરતી યાઈચ્છિક સપાટી વિચારો તો સપાટીમાંથી પસાર થતું ફલક્સ કેટલું હશે ?