चित्रानुसार सकरी गर्दन वाले एक बेलनाकार बर्तन जिसके आधार की त्रिज्या $R$ तथा ऊंचाई $H$ है, गर्दन की ऊंचाई $h$ तथा गर्दन की त्रिज्या $r$ है $\mid$ बर्तन को पानी से तथा गर्दन को अमिश्रणीय (immiscible) तेल से भरा जाता है | पानी तथा तेल के घनत्व क्रमशः $\rho_w$ तथा $\rho_o$ है | चित्र में दिए गए बिदुओं पर दाब का क्या मान होगा ?
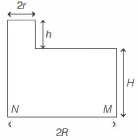
चित्रानुसार सकरी गर्दन वाले एक बेलनाकार बर्तन जिसके आधार की त्रिज्या $R$ तथा ऊंचाई $H$ है, गर्दन की ऊंचाई $h$ तथा गर्दन की त्रिज्या $r$ है $\mid$ बर्तन को पानी से तथा गर्दन को अमिश्रणीय (immiscible) तेल से भरा जाता है | पानी तथा तेल के घनत्व क्रमशः $\rho_w$ तथा $\rho_o$ है | चित्र में दिए गए बिदुओं पर दाब का क्या मान होगा ?

- [KVPY 2017]
- A
$M$ is $g\left(h \rho_0+H \rho_w\right)$
- B
$N$ is $g\left(h \rho_0+H \rho_w\right) \frac{r^2}{R^2}$
- C
$M$ is $g H_w$
- D
$N$ is $g \frac{\rho_w H R^2+\rho_0 h r^2}{R^2+r^2}$
Similar Questions
दो पात्रों के आधारों के क्षेत्रफल समान हैं परंतु आकृतियाँ भिन्न-भिन्न हैं । पहले पात्र में दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है । क्या दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान हैं। यदि ऐसा है तो भार मापने की मशीन पर रखे एक ही ऊँचाई तक जल से भरे दोनों पात्रों के पाठ्यांक भिन्न-भिन्न क्यों होते हैं ?
दो पात्रों के आधारों के क्षेत्रफल समान हैं परंतु आकृतियाँ भिन्न-भिन्न हैं । पहले पात्र में दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है । क्या दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान हैं। यदि ऐसा है तो भार मापने की मशीन पर रखे एक ही ऊँचाई तक जल से भरे दोनों पात्रों के पाठ्यांक भिन्न-भिन्न क्यों होते हैं ?
एक समतल प्लेट ${v_1}$ वेग से, पानी के क्षैतिज पाइप (एक समान अनुप्रस्थकाट) की ओर अभिलम्बवत् गति कर रही है। यह पाइप आयतन $V$ प्रति सैकण्ड की दर से, ${v_2}$ वेग से पानी छोड़ता है। पानी का घनत्व $\rho $ है। माना कि पानी, प्लेट पर उसकी मूल गति के लम्बवत् पड़ता है, तो पानी के कारण प्लेट पर कार्यरत् बल का परिणाम है
एक समतल प्लेट ${v_1}$ वेग से, पानी के क्षैतिज पाइप (एक समान अनुप्रस्थकाट) की ओर अभिलम्बवत् गति कर रही है। यह पाइप आयतन $V$ प्रति सैकण्ड की दर से, ${v_2}$ वेग से पानी छोड़ता है। पानी का घनत्व $\rho $ है। माना कि पानी, प्लेट पर उसकी मूल गति के लम्बवत् पड़ता है, तो पानी के कारण प्लेट पर कार्यरत् बल का परिणाम है
- [IIT 1995]
चित्रानुसार, किसी प्रदर्शन में साइफन (Siphon) का प्रयोग होता है। साइफन में प्रवाहित द्रव का घनत्व $ 1.5 gm/cc $ है। बिन्दु $P $ व $S $ पर दाबों का अतंर होगा
चित्रानुसार, किसी प्रदर्शन में साइफन (Siphon) का प्रयोग होता है। साइफन में प्रवाहित द्रव का घनत्व $ 1.5 gm/cc $ है। बिन्दु $P $ व $S $ पर दाबों का अतंर होगा
एक स्वस्थ मनुष्य की लम्बाई $1.7 \,m$ है तथा उसका औसत रक्तचाप $(BP)$ पारा $Hg$ का $100 \,mm$ है। सामान्यतः हृदय तलवे से $1.3 \,m$ की ऊँचाई पर होता है। मान लेंकि रक्त का घनत्व $10^3 \,kg / m ^3$ है। तलवा क्षेत्र और सिर क्षेत्र के रक्तचापों का अनुपात निम्न के निकटतम होगा। ध्यान दें कि पारे का $100 \,mm , 13.3 \,kPa$ (किलो पास्कल) के बराबर है।
एक स्वस्थ मनुष्य की लम्बाई $1.7 \,m$ है तथा उसका औसत रक्तचाप $(BP)$ पारा $Hg$ का $100 \,mm$ है। सामान्यतः हृदय तलवे से $1.3 \,m$ की ऊँचाई पर होता है। मान लेंकि रक्त का घनत्व $10^3 \,kg / m ^3$ है। तलवा क्षेत्र और सिर क्षेत्र के रक्तचापों का अनुपात निम्न के निकटतम होगा। ध्यान दें कि पारे का $100 \,mm , 13.3 \,kPa$ (किलो पास्कल) के बराबर है।
- [KVPY 2019]
किसी झील की तली में वायु का एक बुलबुला स्थित है, जिसकी त्रिज्या $ r $ है। तली से ऊपरी सतह की ओर जाने पर बुलबुले की त्रिज्या $2r $ हो जाती है। यदि वायुमण्डलीय दाब जल स्तंभ का $P$ सेमी है, तब झील की गहराई है
किसी झील की तली में वायु का एक बुलबुला स्थित है, जिसकी त्रिज्या $ r $ है। तली से ऊपरी सतह की ओर जाने पर बुलबुले की त्रिज्या $2r $ हो जाती है। यदि वायुमण्डलीय दाब जल स्तंभ का $P$ सेमी है, तब झील की गहराई है
