A cylindrical vessel of base radius $R$ and height $H$ has a narrow neck of height $h$ and radius $r$ at one end (see figure). The vessel is filled with water (density $\rho_w$ ) and its neck is filled with immiscible oil (density $\rho_0$ ). Then, the pressure at
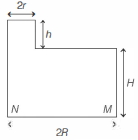
A cylindrical vessel of base radius $R$ and height $H$ has a narrow neck of height $h$ and radius $r$ at one end (see figure). The vessel is filled with water (density $\rho_w$ ) and its neck is filled with immiscible oil (density $\rho_0$ ). Then, the pressure at

- [KVPY 2017]
- A
$M$ is $g\left(h \rho_0+H \rho_w\right)$
- B
$N$ is $g\left(h \rho_0+H \rho_w\right) \frac{r^2}{R^2}$
- C
$M$ is $g H_w$
- D
$N$ is $g \frac{\rho_w H R^2+\rho_0 h r^2}{R^2+r^2}$
Similar Questions
The pressure of confined air is $p$. If the atmospheric pressure is $P$, then
The pressure of confined air is $p$. If the atmospheric pressure is $P$, then
A vertical $U-$ tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density = $1.3 g/cm^3$) column of length $10 $ $cm $ is introduced into one of its arms. Oil of density $0.8 gm/cm^3$ is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the oil column ........ $cm$. Density of mercury = $13.6 g/cm^3$
A vertical $U-$ tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density = $1.3 g/cm^3$) column of length $10 $ $cm $ is introduced into one of its arms. Oil of density $0.8 gm/cm^3$ is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the oil column ........ $cm$. Density of mercury = $13.6 g/cm^3$
Figure shows a container filled with a liquid of density $\rho$. Four points $A, B, C$ and $D$ lie on the diametrically opposite points of a circle as shown. Points $A$ and $C$ lie on vertical line and points $B$ and $D$ lie on horizontal line. The incorrect statement is $\left(p_A, p_B, p_C, p_D\right.$ are absolute pressure at the respective points)
Figure shows a container filled with a liquid of density $\rho$. Four points $A, B, C$ and $D$ lie on the diametrically opposite points of a circle as shown. Points $A$ and $C$ lie on vertical line and points $B$ and $D$ lie on horizontal line. The incorrect statement is $\left(p_A, p_B, p_C, p_D\right.$ are absolute pressure at the respective points)
An open-ended U-tube of uniform cross-sectional area contains water (density $10^3 kg m ^{-3}$ ). Initially the water level stands at $0.29 m$ from the bottom in each arm. Kerosene oil (a water-immiscible liquid) of density $800 kg m ^{-3}$ is added to the left arm until its length is $0.1 m$, as shown in the schematic figure below. The ratio $\left(\frac{h_1}{h_2}\right)$ of the heights of the liquid in the two arms is-
An open-ended U-tube of uniform cross-sectional area contains water (density $10^3 kg m ^{-3}$ ). Initially the water level stands at $0.29 m$ from the bottom in each arm. Kerosene oil (a water-immiscible liquid) of density $800 kg m ^{-3}$ is added to the left arm until its length is $0.1 m$, as shown in the schematic figure below. The ratio $\left(\frac{h_1}{h_2}\right)$ of the heights of the liquid in the two arms is-
- [IIT 2020]
Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill upto a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases ? If so, why do the vessels filled with water to that same height give different readings on a weighing scale ?
Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill upto a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases ? If so, why do the vessels filled with water to that same height give different readings on a weighing scale ?
