દ્વિ-પરિમાણમાં ગતિ કરતાં કણના $(x,\, t)$, $(y,\, t)$ ની આકૃતિઓ નીચે દર્શાવી છે.
જો કણનું દળ $500\, g$ હોય તો તેનાં પર લાગતું બળ (મૂલ્ય અને દિશા) શોધો.
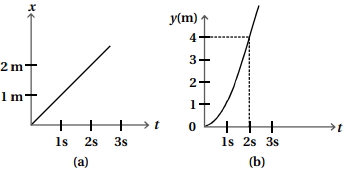
દ્વિ-પરિમાણમાં ગતિ કરતાં કણના $(x,\, t)$, $(y,\, t)$ ની આકૃતિઓ નીચે દર્શાવી છે.
જો કણનું દળ $500\, g$ હોય તો તેનાં પર લાગતું બળ (મૂલ્ય અને દિશા) શોધો.

$x \rightarrow t$ ની આકૃતિ સુરેખ છે તેથી કણની ગતિ નિયમિત છે. અને $x=v_{0} t \quad$ જ્યાં $v_{0}=$ પ્રારંભિક વેગ
$\therefore \frac{d x}{d t}=v_{x}$ $\therefore \frac{1-0}{1-0}=v_{x}=1 ms ^{-1}$
અને પ્રવેગ $a_{x}=0$ કારણ વેગ અચળ છે.
$y \rightarrow t$ ની આકૃતિ પરવલય છે તેથી
$y=t^{2}$
$\therefore \frac{d y}{d t}=2 t$
$\therefore v_{y}=2 t$ અને $\frac{d v_{y}}{d t}=2$
$\therefore a_{y}=2 ms ^{-1}$
$\therefore F = F _{x}+ F _{y}$
$=m a_{x}+m a_{y}$
$=m\left(a_{x}+a_{y}\right)$
$=0.5(0+2)$
$\therefore$$F$$=1.0\,N$
$\tan \theta=\frac{ F _{y}}{ F _{x}}=\frac{2}{0}=$ અનંત
$\therefore \theta=90^{\circ}$ તેથી $y$-અક્ષની દિશામાં
$\therefore \theta=90^{\circ}$ તેથી $y$-અક્ષની દિશામાં
Similar Questions
સ્પ્રિંગના મુક્ત છેડે પર લગાવેલા બ્લોક દ્વારા લાગતા પુનઃસ્થાપન બળને શેના દ્વારા રજૂ કરી શકાય?
સ્પ્રિંગના મુક્ત છેડે પર લગાવેલા બ્લોક દ્વારા લાગતા પુનઃસ્થાપન બળને શેના દ્વારા રજૂ કરી શકાય?
- [NEET 2022]
પદાર્થ સંતુલનમાં છે તેમ ક્યારે કહેવાય ?
પદાર્થ સંતુલનમાં છે તેમ ક્યારે કહેવાય ?
ગતિ અંગેનો ગેલિલિયોનો ઢળતાં સમતલોનો પ્રયોગ વર્ણવો.
ગતિ અંગેનો ગેલિલિયોનો ઢળતાં સમતલોનો પ્રયોગ વર્ણવો.
નીચે આપેલી બળની જોડ સમતુલનમાં છે.
નીચે આપેલી બળની જોડ સમતુલનમાં છે.
વજન $W$ અને ત્રિજ્યા $5\, cm$ ધરાવતા એક નિયમિત ગોલકને એક દોરી સાથે આકૃતિ માં બતાવ્યા મુજબ બાંધેલો છે. તો દોરીમાં તણાવ કેટલું હશે?
વજન $W$ અને ત્રિજ્યા $5\, cm$ ધરાવતા એક નિયમિત ગોલકને એક દોરી સાથે આકૃતિ માં બતાવ્યા મુજબ બાંધેલો છે. તો દોરીમાં તણાવ કેટલું હશે?
- [JEE MAIN 2013]


