Figure shows $(x,\, t)$, $(y,\, t)$ diagram of a particle moving in $2-$ dimensions.
If the particle has a mass of $500\,g$, find the force (direction and magnitude) acting on the particle.
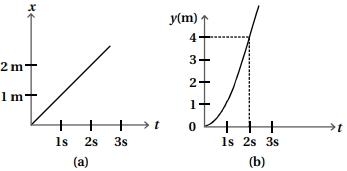
Figure shows $(x,\, t)$, $(y,\, t)$ diagram of a particle moving in $2-$ dimensions.
If the particle has a mass of $500\,g$, find the force (direction and magnitude) acting on the particle.

From figure $(a)$,
Velocity $v=\frac{\Delta x}{\Delta t}=\frac{2-0}{2-0}=1 \mathrm{~m} / \mathrm{s}$ constant velocity.
$\Delta v=0, a_{x}=0$
From figure (b),
Mathematical relation $y=t^{2}$
$v =\frac{d y}{d t}=2 t$
$a=\frac{d v}{d y}=2(1)=2$
$\mathrm{~F}_{x} &=m a_{x} \mid \quad \mathrm{F}_{y}=m a_{y}$
$=0.5(0)$
$=0$
Resultant force,
$\mathrm{F} &=\sqrt{\mathrm{F}_{x}^{2}+\mathrm{F}_{y}^{2}}$
$=\sqrt{0^{2}+1^{2}}$
$=1 \mathrm{~N}$
Similar Questions
Three blocks of masses $2 \,kg, 3 \,kg$ and $5\, kg$ are connected to each other with light string and are then placed on a frictionless surface as shown in the figure. The system is pulled by a force $F = 10N,$ then tension ${T_1} = $ .......... $N$
Three blocks of masses $2 \,kg, 3 \,kg$ and $5\, kg$ are connected to each other with light string and are then placed on a frictionless surface as shown in the figure. The system is pulled by a force $F = 10N,$ then tension ${T_1} = $ .......... $N$
Write important guidance for solving problems in mechanics.
Write important guidance for solving problems in mechanics.
There are four forces acting at a point $P$ produced by strings as shown in figure, point $P$ is at rest. The forces $F_1$ and $F_2$ are respectively:-
A rope of length $5\,m$ is kept on frictionless surface and a force of $5\,N$ is applied to one of its end. Find tension in the rope at $1\,m $ from this end ......... $N$
A rope of length $5\,m$ is kept on frictionless surface and a force of $5\,N$ is applied to one of its end. Find tension in the rope at $1\,m $ from this end ......... $N$
Two objects $A$ and $B$ each of mass $m$ are connected by a light inextensible string. They are restricted to move on a frictionless ring of radius $R$ in a vertical plane (as shown in fig). The objects are released from rest at the position shown. Then, the tension in the cord just after release is
Two objects $A$ and $B$ each of mass $m$ are connected by a light inextensible string. They are restricted to move on a frictionless ring of radius $R$ in a vertical plane (as shown in fig). The objects are released from rest at the position shown. Then, the tension in the cord just after release is


