સાદા વિધુતભાર વિતરણની ક્ષેત્રરેખાઓ દોરો.
સાદા વિધુતભાર વિતરણની ક્ષેત્રરેખાઓ દોરો.
ક્ષેત્રરેખાઓની ચિત્રાત્મક રજૂઆત ફેરેડે નામના વૈજ્ઞાનિકે વિદ્યુતભારોના તંત્રની આસપાસના વિદ્યુતક્ષેત્રને દૃશ્યમાન કરવા માટે કરી હતી. આ ક્ષેત્રરેખાઓને ફેરેડેએ બળરેખાઓ કહી હતી.
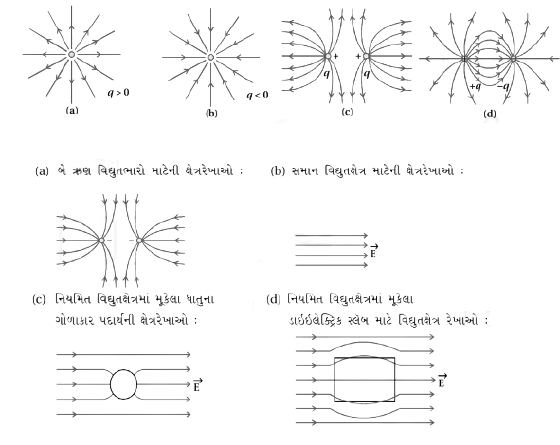
કેટલાંક સાદા વિદ્યુતભાર વિતરણની ક્ષેત્રરેખાઓ નીચે આકૃતિમાં દર્શાવી છે. આ આકૃતિઓ સમતલમાં દર્શાવી છે પણ તે ખરેખર ત્રિપરિમાણમાં હોય છે.
આકૃતિ $(a)$ માં ધન વિદ્યુતભારની ક્ષેત્રરેખાઓ છે.
આકૃતિ $(b)$ માં ઋણ વિદ્યુતભારની ક્ષેત્રરેખાઓ છે.
આકૃતિ $(c)$ માં બે ધન વિધુતભારની ક્ષેત્રરેખાઓ છે.
આકૃતિ $(d)$ માં વિદ્યુત ડાઇપોલ માટેની ક્ષેત્રરેખાઓ છે.
Similar Questions
આકૃતિમાં વિદ્યુતક્ષેત્રના ઘટકો $E_{x}=\alpha x^{1 / 2}, E_{y}=E_{z}=0$ છે. જ્યાં, $\alpha=800 \;N / C\, m ^{1 / 2} .$ $(a)$ ઘનમાંથી ફ્લક્સ અને $(b)$ ઘનની અંદરના વિદ્યુતભારની ગણતરી કરો. $a=0.1 \;m$ ધારો.
આકૃતિમાં વિદ્યુતક્ષેત્રના ઘટકો $E_{x}=\alpha x^{1 / 2}, E_{y}=E_{z}=0$ છે. જ્યાં, $\alpha=800 \;N / C\, m ^{1 / 2} .$ $(a)$ ઘનમાંથી ફ્લક્સ અને $(b)$ ઘનની અંદરના વિદ્યુતભારની ગણતરી કરો. $a=0.1 \;m$ ધારો.
વિદ્યુત ફલક્સ સદિશ છે કે અદિશ ? તે સમજાવો ?
વિદ્યુત ફલક્સ સદિશ છે કે અદિશ ? તે સમજાવો ?
એક લાંબા નળાકારમાં $\rho \;Cm ^{-3}$ ધનતા ધરાવતો વિદ્યુતભાર નિયમિત રીતે વહેંચાયેલો છે. $Vm ^{-1}$ હશે.નળાકારની અંદર તેની અક્ષથી $ x=\frac{2 \varepsilon_{0}}{\rho} \,m$ અંતરે વિદ્યુતક્ષેત્ર ગણો. વિદ્યુતક્ષેત્રનું મૂલ્ય ........ $Vm ^{-1}$ હશે.
એક લાંબા નળાકારમાં $\rho \;Cm ^{-3}$ ધનતા ધરાવતો વિદ્યુતભાર નિયમિત રીતે વહેંચાયેલો છે. $Vm ^{-1}$ હશે.નળાકારની અંદર તેની અક્ષથી $ x=\frac{2 \varepsilon_{0}}{\rho} \,m$ અંતરે વિદ્યુતક્ષેત્ર ગણો. વિદ્યુતક્ષેત્રનું મૂલ્ય ........ $Vm ^{-1}$ હશે.
- [JEE MAIN 2022]
ત્રણ ધન $q$ મૂલ્યના વિજભાર ત્રિકોણના શિરોબિંદુ પર પડેલા છે.તેની પરિણામી બળ રેખા કેવી દેખાય?
ત્રણ ધન $q$ મૂલ્યના વિજભાર ત્રિકોણના શિરોબિંદુ પર પડેલા છે.તેની પરિણામી બળ રેખા કેવી દેખાય?
- [AIEEE 2012]
સમઘનના કેન્દ્ર પર $Q\;\mu C$ વિદ્યુતભાર મૂકેલો છે. તો સમઘનના કોઈ પણ પૃષ્ઠમાંથી પસાર થતું ફ્લક્સ કેટલું હશે?
સમઘનના કેન્દ્ર પર $Q\;\mu C$ વિદ્યુતભાર મૂકેલો છે. તો સમઘનના કોઈ પણ પૃષ્ઠમાંથી પસાર થતું ફ્લક્સ કેટલું હશે?
- [AIPMT 2001]


