एकसमान तार को मोड़कर $R$ त्रिज्या का एक वृत्त बनाया गया है। धारा $I$ बिन्दु $A$ पर प्रवेश करती है और बिन्दु $C$ से निकल जाती है, जैसा कि चित्र में दिखाया गया है। यदि लम्बाई $ ABC$ लम्बाई $ADC$ की आधी है, तो केन्द्र $O$ पर चुम्बकीय क्षेत्र का मान होगा
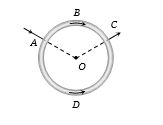
एकसमान तार को मोड़कर $R$ त्रिज्या का एक वृत्त बनाया गया है। धारा $I$ बिन्दु $A$ पर प्रवेश करती है और बिन्दु $C$ से निकल जाती है, जैसा कि चित्र में दिखाया गया है। यदि लम्बाई $ ABC$ लम्बाई $ADC$ की आधी है, तो केन्द्र $O$ पर चुम्बकीय क्षेत्र का मान होगा

- A
शून्य
- B
$\frac{{{\mu _0}I}}{{2R}}$
- C
$\frac{{{\mu _0}I}}{{4R}}$
- D
$\frac{{{\mu _0}I}}{{6R}}$
Similar Questions
$r$ त्रिज्या की वर्तुल कुण्डली में $I$ धारा प्रवाहित हो रही है। इसके केन्द्र पर क्षेत्र की तीव्रता है
$r$ त्रिज्या की वर्तुल कुण्डली में $I$ धारा प्रवाहित हो रही है। इसके केन्द्र पर क्षेत्र की तीव्रता है
$R$ त्रिज्या के वृत्तीय चाप खण्ड में से $i$ धारा प्रवाहित हो रही है। यदि चाप खण्ड अपने केन्द्र पर $3\pi /2$ रेडियन का कोण बनाता है, तो इसके केन्द्र पर चुम्बकीय क्षेत्र होगा
$R$ त्रिज्या के वृत्तीय चाप खण्ड में से $i$ धारा प्रवाहित हो रही है। यदि चाप खण्ड अपने केन्द्र पर $3\pi /2$ रेडियन का कोण बनाता है, तो इसके केन्द्र पर चुम्बकीय क्षेत्र होगा
$1000$ फेरों वाली अच्छी तरह से कसी हुई एक कुंडली का औसत त्रिज्या $62.8\,cm$ है। यदि कुंडली के तार में $1\,A$ की धारा प्रवाहित है, तो कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र का मान लगभग होगा : (मुक्त आकाश की चुम्बकशीलता $=4 \pi \times 10^{-7}\,H / m$ )
$1000$ फेरों वाली अच्छी तरह से कसी हुई एक कुंडली का औसत त्रिज्या $62.8\,cm$ है। यदि कुंडली के तार में $1\,A$ की धारा प्रवाहित है, तो कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र का मान लगभग होगा : (मुक्त आकाश की चुम्बकशीलता $=4 \pi \times 10^{-7}\,H / m$ )
- [NEET 2022]
नीचे दिये गए चित्र में एक चौथाई वृत्ताकर कुंडली को जोड़ा गया है जिसकी आंतरिक और बाहरी त्रिज्या क्रमशः $r$ और $R$ है। इस व्यवस्था का संयुक्त केंद्र $C$ है और कुंडली में $I$ धारा प्रवाहित होती है। यदि निर्वात की पारगम्यता (permeability of vacuum) $\mu_0$ है तो $C$ पर चुम्बकीय क्षेत्र होगा
नीचे दिये गए चित्र में एक चौथाई वृत्ताकर कुंडली को जोड़ा गया है जिसकी आंतरिक और बाहरी त्रिज्या क्रमशः $r$ और $R$ है। इस व्यवस्था का संयुक्त केंद्र $C$ है और कुंडली में $I$ धारा प्रवाहित होती है। यदि निर्वात की पारगम्यता (permeability of vacuum) $\mu_0$ है तो $C$ पर चुम्बकीय क्षेत्र होगा
- [KVPY 2013]
दी गई व्यवस्था में बिन्दु $O$ पर चुम्बकीय क्षेत्र है
दी गई व्यवस्था में बिन्दु $O$ पर चुम्बकीय क्षेत्र है
