A uniform wire is bent in the form of a circle of radius $R$. A current $I$ enters at $A$ and leaves at $C$ as shown in the figure :If the length $ABC$ is half of the length $ADC,$ the magnetic field at the centre $O$ will be
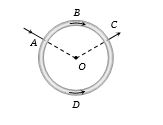
A uniform wire is bent in the form of a circle of radius $R$. A current $I$ enters at $A$ and leaves at $C$ as shown in the figure :If the length $ABC$ is half of the length $ADC,$ the magnetic field at the centre $O$ will be

- A
Zero
- B
$\frac{{{\mu _0}I}}{{2R}}$
- C
$\frac{{{\mu _0}I}}{{4R}}$
- D
$\frac{{{\mu _0}I}}{{6R}}$
Similar Questions
Current $I$ is flowing along the path $ABCDA$ consisting of four edges of a cube (figure $-a$), produces a magnetic field $B_0$ at the centre of the cube. Find the magnetic field $B$ produced at the center of the cube by a current $I$ flowing along the path of the six edges $ABCGHEA$ (figure $b$)
Current $I$ is flowing along the path $ABCDA$ consisting of four edges of a cube (figure $-a$), produces a magnetic field $B_0$ at the centre of the cube. Find the magnetic field $B$ produced at the center of the cube by a current $I$ flowing along the path of the six edges $ABCGHEA$ (figure $b$)
In the figure, what is the magnetic field at the point $O$
In the figure, what is the magnetic field at the point $O$
A non-planar loop of conducting wire carrying a current $I$ is placed as shown in the figure. Each of the straight sections of the loop is of length $2a$. The magnetic field due to this loop at the point $P$ $(a,0,a)$ points in the direction
A non-planar loop of conducting wire carrying a current $I$ is placed as shown in the figure. Each of the straight sections of the loop is of length $2a$. The magnetic field due to this loop at the point $P$ $(a,0,a)$ points in the direction
- [IIT 2001]
A coil having $N$ turns is wound tightly in the form of a spiral with inner and outer radii $a$ and $b$ respectively. When a current $i$ passes through the coil, the magnetic field at the centre is
A coil having $N$ turns is wound tightly in the form of a spiral with inner and outer radii $a$ and $b$ respectively. When a current $i$ passes through the coil, the magnetic field at the centre is
An infinitely long straight conductor is bent into the shape as shown in the figure. It carries a current of $i$ $ampere$ and the radius of the circular loop is $r$ $metre$. Then the magnetic induction at its centre will be
An infinitely long straight conductor is bent into the shape as shown in the figure. It carries a current of $i$ $ampere$ and the radius of the circular loop is $r$ $metre$. Then the magnetic induction at its centre will be
