આકૃતિ જુઓ. $4\; kg$ દળ એક સમક્ષિતિજ સમતલ પર રહેલ છે. સમતલને સમક્ષિતિજ સાથે ક્રમશ: ઢળતું કરતાં $\theta= 15^o$ એ તે દળ ખસવાની શરૂઆત કરે છે. બ્લૉક અને સપાટી વચ્ચેનો સ્થિત ઘર્ષણાંક કેટલો હશે ?
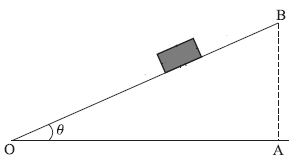
આકૃતિ જુઓ. $4\; kg$ દળ એક સમક્ષિતિજ સમતલ પર રહેલ છે. સમતલને સમક્ષિતિજ સાથે ક્રમશ: ઢળતું કરતાં $\theta= 15^o$ એ તે દળ ખસવાની શરૂઆત કરે છે. બ્લૉક અને સપાટી વચ્ચેનો સ્થિત ઘર્ષણાંક કેટલો હશે ?
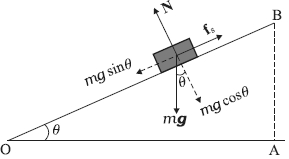
ઢાળ પર સ્થિર રહેલા દળ $m$ પર $(i)$ વજન $mg$ અધો દિશામાં લાગે $(ii)$ સમતલ વડે બ્લૉક પર લંબ બળ $N$ લાગે $(iii)$ અપેક્ષિત ગતિનો વિરોધ કરતું સ્થિત ઘર્ષણબળ $f_{ s }$ લાગે. સંતુલનમાં આ બધાં બળોનું પરિણામી બળ શૂન્ય બનવું જોઈએ. દર્શાવેલી બે દિશાઓમાં $mg$ નાં ઘટકો લેતાં,
$m g \sin \theta=f_{s}, \quad m g \cos \theta=N$
જેમ જેમ $\theta $ વધે છે તેમ તેમ સ્વનિયમન કરતું ઘર્ષણબળ વધે છે અને $\theta = {\theta _{\max }}$, માટે ${f_s}$ તેનું મહત્તમ મૂલ્ય પ્રાપ્ત કરે છે $\left(f_{s}\right)_{\max }=\mu_{s} N$
આથી, $\tan \theta_{\max }=\mu_{s}$ અથવા $\theta_{\max }=\tan ^{-1} \mu_{s}$
જ્યારે $\theta$, $\theta_{\max }$ કરતાં સહેજ જ વધે કે તરત બ્લૉક પર સહેજ ચોખ્ખું બળ લાગે અને તે ખસવા લાગે. એ નોંધો કે $\theta_{\max }$ માત્ર $\mu_{ s }$ પર આધારિત છે પણ બ્લૉકના દળ પર આધારિત નથી.
$\quad \theta_{\max }=15^{\circ}$ માટે
$\mu_{s}=\tan 15^{\circ}$
$=0.27$
Similar Questions
એક ફૂટબૉલ ખેલાડી દક્ષિણ તરફ ગતિ કરે છે અને વિરોધીને અવગણવા અચાનક તે તેટલી ઝડપથી પૂર્વ તરફ વળે છે. ખેલાડી પર વળતી વખતે લાગતું ઘર્ષણ બળ $........$ હશે.
એક ફૂટબૉલ ખેલાડી દક્ષિણ તરફ ગતિ કરે છે અને વિરોધીને અવગણવા અચાનક તે તેટલી ઝડપથી પૂર્વ તરફ વળે છે. ખેલાડી પર વળતી વખતે લાગતું ઘર્ષણ બળ $........$ હશે.
- [NEET 2023]
$0.5\, kg$ દળ ધરાવતાં લાકડાનાં ચોસલા અને ઊભી ખરબચડી દિવાલ વચ્ચે સ્થિત ઘર્ષણાંક $0.2$ છે. બ્લોક દિવાલ સાથે ચિપકેલો (ચોટેલો) રહે તે માટે લગાવવું પડતું સમક્ષિતિજ બળ ગણો ............. $N.$ $\left[g=10\, ms ^{-2}\right]$
$0.5\, kg$ દળ ધરાવતાં લાકડાનાં ચોસલા અને ઊભી ખરબચડી દિવાલ વચ્ચે સ્થિત ઘર્ષણાંક $0.2$ છે. બ્લોક દિવાલ સાથે ચિપકેલો (ચોટેલો) રહે તે માટે લગાવવું પડતું સમક્ષિતિજ બળ ગણો ............. $N.$ $\left[g=10\, ms ^{-2}\right]$
- [JEE MAIN 2021]
આકૃતિ એક સમક્ષિતિજ કન્વેયર (વહન કરાવતા) બૅલ્ટ, જે $1\; m s^{-2}$ થી પ્રવેગિત થાય છે, તેના પર બૅલ્ટની સાપેક્ષે ઊભેલો એક સ્થિર માણસ દર્શાવેલ છે. માણસ પર ચોખ્ખું (પરિણામી બળ) કેટલું હશે ? જો માણસના બૂટ અને બૅલ્ટ વચ્ચેનો સ્થિત ઘર્ષણાંક $0.2$ હોય, તો બૅલ્ટના કેટલા પ્રવેગ સુધી માણસ બૅલ્ટની સાપેક્ષે સ્થિર ઊભો રહી શકે ? ( માણસનું દળ $= 65 \;kg$ )
આકૃતિ એક સમક્ષિતિજ કન્વેયર (વહન કરાવતા) બૅલ્ટ, જે $1\; m s^{-2}$ થી પ્રવેગિત થાય છે, તેના પર બૅલ્ટની સાપેક્ષે ઊભેલો એક સ્થિર માણસ દર્શાવેલ છે. માણસ પર ચોખ્ખું (પરિણામી બળ) કેટલું હશે ? જો માણસના બૂટ અને બૅલ્ટ વચ્ચેનો સ્થિત ઘર્ષણાંક $0.2$ હોય, તો બૅલ્ટના કેટલા પ્રવેગ સુધી માણસ બૅલ્ટની સાપેક્ષે સ્થિર ઊભો રહી શકે ? ( માણસનું દળ $= 65 \;kg$ )
કાર એક સમક્ષિતિજ રોડ પર $V_o $ વેગ થી ગતિ કરે છે ટાયર અને રોડ વચ્ચે નો ઘર્ષણાક $\mu $ છે તો કાર ને ઊભી રાખવા માટે નું ન્યૂનતમ કેટલુ અંતર કાપ્શે?
કાર એક સમક્ષિતિજ રોડ પર $V_o $ વેગ થી ગતિ કરે છે ટાયર અને રોડ વચ્ચે નો ઘર્ષણાક $\mu $ છે તો કાર ને ઊભી રાખવા માટે નું ન્યૂનતમ કેટલુ અંતર કાપ્શે?
જ્યારે એક સિક્કાને ભ્રમણ કરતા ટેબલ પર તેના કેન્દ્રથી $1\,cm$ અંતરે મૂકવામાં આવે છે ત્યારે જ તે સરકવાનું શરૂ કરે છે. જો ભ્રમણ કરતા ટેબલનો કોણીય વેગ અડધો કરવામાં આવે, તો ........ $cm$ તે અંતરે રાખતા સરકશે.
જ્યારે એક સિક્કાને ભ્રમણ કરતા ટેબલ પર તેના કેન્દ્રથી $1\,cm$ અંતરે મૂકવામાં આવે છે ત્યારે જ તે સરકવાનું શરૂ કરે છે. જો ભ્રમણ કરતા ટેબલનો કોણીય વેગ અડધો કરવામાં આવે, તો ........ $cm$ તે અંતરે રાખતા સરકશે.
- [JEE MAIN 2023]