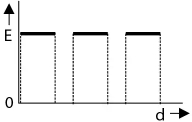
Two thin dielectric slabs of dielectric constants $K_1$ and $K_2$ $(K_1 < K_2)$ are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field $E$ between the plates with distance $d$ as measured from plate $P$ is correctly shown by

Two thin dielectric slabs of dielectric constants $K_1$ and $K_2$ $(K_1 < K_2)$ are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field $E$ between the plates with distance $d$ as measured from plate $P$ is correctly shown by

- [AIPMT 2014]
- A

- B

- C

- D
Similar Questions
The distance between plates of a parallel plate capacitor is $5d$. Let the positively charged plate is at $ x=0$ and negatively charged plate is at $x=5d$. Two slabs one of conductor and other of a dielectric of equal thickness $d$ are inserted between the plates as shown in figure. Potential versus distance graph will look like :
The distance between plates of a parallel plate capacitor is $5d$. Let the positively charged plate is at $ x=0$ and negatively charged plate is at $x=5d$. Two slabs one of conductor and other of a dielectric of equal thickness $d$ are inserted between the plates as shown in figure. Potential versus distance graph will look like :
A parallel plate capacitor of area ' $A$ ' plate separation ' $d$ ' is filled with two dielectrics as shown. What is the capacitance of the arrangement?
A parallel plate capacitor of area ' $A$ ' plate separation ' $d$ ' is filled with two dielectrics as shown. What is the capacitance of the arrangement?
The potential gradient at which the dielectric of a condenser just gets punctured is called
The potential gradient at which the dielectric of a condenser just gets punctured is called
A spherical capacitor has an inner sphere of radius $12 \;cm$ and an outer sphere of radius $13\; cm .$ The outer sphere is earthed and the inner sphere is given a charge of $2.5\; \mu \,C .$ The space between the concentric spheres is filled with a liquid of dielectric constant $32$
$(a)$ Determine the capacitance of the capacitor.
$(b)$ What is the potential of the inner sphere?
$(c)$ Compare the capacitance of this capacitor with that of an isolated sphere of radius $12 \;cm .$ Explain why the latter is much smaller.
A spherical capacitor has an inner sphere of radius $12 \;cm$ and an outer sphere of radius $13\; cm .$ The outer sphere is earthed and the inner sphere is given a charge of $2.5\; \mu \,C .$ The space between the concentric spheres is filled with a liquid of dielectric constant $32$
$(a)$ Determine the capacitance of the capacitor.
$(b)$ What is the potential of the inner sphere?
$(c)$ Compare the capacitance of this capacitor with that of an isolated sphere of radius $12 \;cm .$ Explain why the latter is much smaller.
An uncharged parallel plate capacitor having a dielectric of constant $K$ is connected to a similar air-cored parallel capacitor charged to a potential $V$. The two share the charge and the common potential is $V'$. The dielectric constant $K$ is
An uncharged parallel plate capacitor having a dielectric of constant $K$ is connected to a similar air-cored parallel capacitor charged to a potential $V$. The two share the charge and the common potential is $V'$. The dielectric constant $K$ is
