Three identical spheres, each of mass $M ,$ are placed at the corners of a right angle triangle with mutually perpendicular sides equal to $2 \;m$ (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of centre of mass.
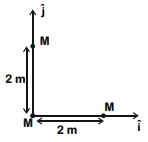
Three identical spheres, each of mass $M ,$ are placed at the corners of a right angle triangle with mutually perpendicular sides equal to $2 \;m$ (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of centre of mass.

- [NEET 2020]
- A
$\frac{4}{3}(\hat{i}+\hat{j})$
- B
$2(\hat{i}+\hat{j})$
- C
$(\hat{i}+\hat{j})$
- D
$\frac{2}{3}(\hat{i}+\hat{j})$
Similar Questions
$(n - 1)$ equal point masses each of mass $m$ are placed at the vertices of a regular $n-$ polygon. The vacant vertex has a position vector $a$ with respect to the centre of the polygon. Find the position vector of centre of mass.
$(n - 1)$ equal point masses each of mass $m$ are placed at the vertices of a regular $n-$ polygon. The vacant vertex has a position vector $a$ with respect to the centre of the polygon. Find the position vector of centre of mass.
Mass is distributed uniformly over a thin square plate. If two end points of diagonal are $(-2, 0)$ and $(2, 2)$, what are the coordinates of centre of mass of plate ?
Mass is distributed uniformly over a thin square plate. If two end points of diagonal are $(-2, 0)$ and $(2, 2)$, what are the coordinates of centre of mass of plate ?
When does a body (system) have different centre of gravity and centre of mass ?
When does a body (system) have different centre of gravity and centre of mass ?
A uniform square plate abcd has a mass of $1 \,kg$. If two point masses each of $20 \,g$ are placed at the corners $b$ and $c$ as shown, then the centre of mass shifts on the line
A uniform square plate abcd has a mass of $1 \,kg$. If two point masses each of $20 \,g$ are placed at the corners $b$ and $c$ as shown, then the centre of mass shifts on the line
Sector of a circular plate shown in figure has position of centre of mass at $y_{CM} =$
Sector of a circular plate shown in figure has position of centre of mass at $y_{CM} =$
