Five charges $+q,+5 q,-2 q,+3 q$ and $-4 q$ are situated as shown in the figure.
The electric flux due to this configuration through the surface $S$ is
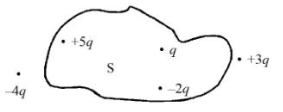
Five charges $+q,+5 q,-2 q,+3 q$ and $-4 q$ are situated as shown in the figure.
The electric flux due to this configuration through the surface $S$ is
- [JEE MAIN 2024]
- A
$\frac{5 q}{\epsilon_0}$
- B
$\frac{4 q}{\epsilon_0}$
- C
$\frac{3 q}{\epsilon_0}$
- D
$\frac{q}{\epsilon_0}$
Similar Questions
Each of two large conducting parallel plates has one sided surface area $A$. If one of the plates is given a charge $Q$ whereas the other is neutral, then the electric field at a point in between the plates is given by
Each of two large conducting parallel plates has one sided surface area $A$. If one of the plates is given a charge $Q$ whereas the other is neutral, then the electric field at a point in between the plates is given by
A charge $q$ is located at the centre of a cube. The electric flux through any face is
A charge $q$ is located at the centre of a cube. The electric flux through any face is
- [AIPMT 2003]
A cylinder of radius $R$ and length $L$ is placed in a uniform electric field $E$ parallel to the cylinder axis. The total flux for the surface of the cylinder is given by-
A cylinder of radius $R$ and length $L$ is placed in a uniform electric field $E$ parallel to the cylinder axis. The total flux for the surface of the cylinder is given by-
Consider the charge configuration and spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface the electric field will be due to
Consider the charge configuration and spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface the electric field will be due to
- [IIT 2004]
$q_1, q_2, q_3$ and $q_4$ are point charges located at point as shown in the figure and $S$ is a spherical Gaussian surface of radius $R$. Which of the following is true according to the Gauss's law
$q_1, q_2, q_3$ and $q_4$ are point charges located at point as shown in the figure and $S$ is a spherical Gaussian surface of radius $R$. Which of the following is true according to the Gauss's law