Figure shows three vectors $p , q$ and $r$, where $C$ is the mid point of $A B$. Then, which of the following relation is correct?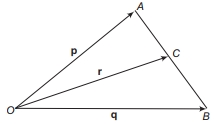

- A$p+q=2 r$
- B$p+q=r$
- C$p-q=2 r$
- D$p-q=r$
Similar Questions
$\vec{A}$ is a vector of magnitude $2.7$ units due east. What is the magnitude and direction of vector $4 \vec{A}$ ?
$\vec{A}$ is a vector of magnitude $2.7$ units due east. What is the magnitude and direction of vector $4 \vec{A}$ ?
Let $\overrightarrow C = \overrightarrow A + \overrightarrow B$
$(A)$ It is possible to have $| \overrightarrow C | < | \overrightarrow A |$ and $ | \overrightarrow C | < | \overrightarrow B|$
$(B)$ $|\overrightarrow C |$ is always greater than $|\overrightarrow A |$
$(C)$ $|\overrightarrow C |$ may be equal to $|\overrightarrow A | + |\overrightarrow B|$
$(D)$ $|\overrightarrow C |$ is never equal to $|\overrightarrow A | + |\overrightarrow B|$
Which of the above is correct
Let $\overrightarrow C = \overrightarrow A + \overrightarrow B$
$(A)$ It is possible to have $| \overrightarrow C | < | \overrightarrow A |$ and $ | \overrightarrow C | < | \overrightarrow B|$
$(B)$ $|\overrightarrow C |$ is always greater than $|\overrightarrow A |$
$(C)$ $|\overrightarrow C |$ may be equal to $|\overrightarrow A | + |\overrightarrow B|$
$(D)$ $|\overrightarrow C |$ is never equal to $|\overrightarrow A | + |\overrightarrow B|$
Which of the above is correct
How many minimum number of non-zero vectors in different planes can be added to give zero resultant
How many minimum number of non-zero vectors in different planes can be added to give zero resultant
Two forces acting on point $A$ along their side and having magnitude reciprocal to length of side then resultant of these forces will be proportional to
Two forces acting on point $A$ along their side and having magnitude reciprocal to length of side then resultant of these forces will be proportional to
Let $\overrightarrow C = \overrightarrow A + \overrightarrow B $ then
Let $\overrightarrow C = \overrightarrow A + \overrightarrow B $ then
