ઘન પદાર્થનું દ્રવ્યમાન કેન્દ્ર નક્કી કરવાની સ | vedclass

Name: PDF Generator App | JEE NEET Paper Generator | Vedclass
Brand: Vedclass
Rating: 5 (35 reviews)

Question

ઘન પદાર્થ અસંખ્ય સૂક્ષ્મ કણો (પરમાણુઓ, અણુંઓ)નો બનેલો છે. આ કણો ધન પદર્થમાં સતત રીતે વિતરિત થયેલાં હોય છે.

આકૃતિમાં દર્શાવ્યાં અનુસાર, ધારો કે $n$

Vedclass · Accepted Answer

Vedclass · Answer

ઘન પદાર્થ અસંખ્ય સૂક્ષ્મ કણો (પરમાણુઓ, અણુંઓ)નો બનેલો છે. આ કણો ધન પદર્થમાં સતત રીતે વિતરિત થયેલાં હોય છે.

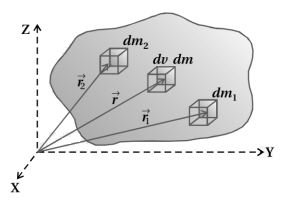
આકૃતિમાં દર્શાવ્યાં અનુસાર, ધારો કે $n$ સૂક્ષ્મ દળ ખંડોનો બનેલો છે અને દરેક દળ ખંડનું દળ $\Delta m$ છે. આ $\Delta m$ દળ ખંડનો સ્થાન સદિશ $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ છે.

સમગ્ર ધન પદર્થને $\Delta m_{1}, \Delta m_{2}, \ldots, \Delta m_{n}$ જેવાં દળ ખંડોનો બનેલો ગણી શકાય. આ દળ ખંડોના સ્થાન સદિશ અનુક્રમે $\overrightarrow{r_{1}}, \overrightarrow{r_{2}}, \ldots, \overrightarrow{r_{n}} छ$

ધન પદાર્થના દ્રવ્યમાન કેન્દ્રનો સ્થાન સદિશ,

$\overrightarrow{ R }=\frac{\Delta m_{1} \overrightarrow{r_{1}}+\Delta m_{2} \overrightarrow{r_{2}}+\Delta m_{n} \overrightarrow{r_{n}}}{\Delta m_{1}+\Delta m_{2}+\ldots+\Delta m_{n}}$

$	herefore$ દ્રવ્યમાન કેન્દ્રના યામો,

$X$$=\frac{\Sigma\left(\Delta m_{i}ight) x_{i}}{\Sigma \Delta m_{i}}$

$Y=\frac{\Sigma \Delta m_{i} y_{i}}{\Sigma \Delta m_{i}}$

$Z=\frac{\Sigma \Delta m_{i} z_{i}}{\Sigma \Delta m_{i}}$

ઘન પદાર્થનું દ્રવ્યમાન કેન્દ્ર નક્કી કરવાની સૈદ્ધાંતિક રીત વર્ણવો.

Similar Questions