A uniform rod of length $l$ is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is $T(x)$ at a distance $x$ from the axis, then which of the following graphs depicts it most closely?
A uniform rod of length $l$ is being rotated in a horizontal plane with a constant angular speed about an axis passing through one of its ends. If the tension generated in the rod due to rotation is $T(x)$ at a distance $x$ from the axis, then which of the following graphs depicts it most closely?
- [JEE MAIN 2019]
- A

- B

- C
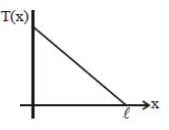
- D

Similar Questions
A cyclist on a level road takes a sharp circular turn of radius $3 \;m \;\left( g =10 \;ms ^{-2}\right)$. If the coefficient of static friction between the cycle tyres and the road is $0.2$, at which of the following speeds will the cyclist not skid while taking the turn?
A cyclist on a level road takes a sharp circular turn of radius $3 \;m \;\left( g =10 \;ms ^{-2}\right)$. If the coefficient of static friction between the cycle tyres and the road is $0.2$, at which of the following speeds will the cyclist not skid while taking the turn?
- [NEET 2017]
A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance $'r'$. The speed of the particle is
A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance $'r'$. The speed of the particle is
A gramophone record is revolving with an angular velocity $\omega$. A coin is placed at a distance $r$ from the centre of the record. The static coefficient of friction is $\mu .$ The coin will revolve with the record if
A gramophone record is revolving with an angular velocity $\omega$. A coin is placed at a distance $r$ from the centre of the record. The static coefficient of friction is $\mu .$ The coin will revolve with the record if
- [AIPMT 2010]
A body of mass $1\, kg$ tied to one end of string is revolved in a horizontal circle of radius $0.1\, m$ with a speed of $3$ revolution/sec, assuming the effect of gravity is negligible, then linear velocity, acceleration and tension in the string will be
A body of mass $1\, kg$ tied to one end of string is revolved in a horizontal circle of radius $0.1\, m$ with a speed of $3$ revolution/sec, assuming the effect of gravity is negligible, then linear velocity, acceleration and tension in the string will be
An unbanked curve has a radius of $60\,m$. The maximum speed at which a car can make a turn if the coefficient of static friction is $0.75$, is ...... $m/s$
An unbanked curve has a radius of $60\,m$. The maximum speed at which a car can make a turn if the coefficient of static friction is $0.75$, is ...... $m/s$
