A parallel plate capacitor with plate area $A$ and plate separation $d =2 \,m$ has a capacitance of $4 \,\mu F$. The new capacitance of the system if half of the space between them is filled with a dielectric material of dielectric constant $K =3$ (as shown in figure) will be .........$ \mu \,F$
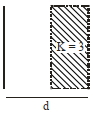
A parallel plate capacitor with plate area $A$ and plate separation $d =2 \,m$ has a capacitance of $4 \,\mu F$. The new capacitance of the system if half of the space between them is filled with a dielectric material of dielectric constant $K =3$ (as shown in figure) will be .........$ \mu \,F$

- [JEE MAIN 2022]
- A
$2$
- B
$32$
- C
$6$
- D
$8$
Similar Questions
In the figure a capacitor is filled with dielectrics. The resultant capacitance is
In the figure a capacitor is filled with dielectrics. The resultant capacitance is
The plates of parallel plate capacitor are charged upto $100\;V$. A $2\,mm$ thick plate is inserted between the plates. Then to maintain the same potential difference, the distance between the plates is increased by $1.6\;mm$. The dielectric constant of the plate is
Two parallel plate capacitors of capacity $C$ and $3\,C$ are connected in parallel combination and charged to a potential difference $18\,V$. The battery is then disconnected and the space between the plates of the capacitor of capacity $C$ is completely filled with a material of dielectric constant $9$. The final potential difference across the combination of capacitors will be $V$
Two parallel plate capacitors of capacity $C$ and $3\,C$ are connected in parallel combination and charged to a potential difference $18\,V$. The battery is then disconnected and the space between the plates of the capacitor of capacity $C$ is completely filled with a material of dielectric constant $9$. The final potential difference across the combination of capacitors will be $V$
- [JEE MAIN 2022]
A parallel plate capacitor is connected to a battery. The quantities charge, voltage, electric field and energy associated with the capacitor are given by $Q_0, V_0, E_0$ and $U_0$ respectively. A dielectric slab is introduced between plates of capacitor but battery is still in connection. The corresponding quantities now given by $Q, V, E$ and $U$ related to previous ones are
A parallel plate capacitor is connected to a battery. The quantities charge, voltage, electric field and energy associated with the capacitor are given by $Q_0, V_0, E_0$ and $U_0$ respectively. A dielectric slab is introduced between plates of capacitor but battery is still in connection. The corresponding quantities now given by $Q, V, E$ and $U$ related to previous ones are
A parallel-plate capacitor of area $A,$ plate separation $d$ and capacitance $C$ is filled with four dielectric materials having dielectric constants $K_1,K_2,K_3$ and $K_4$ as shown in the figure. If a single dielectric material is to be used to have the same capacitance $C$ in this capacitor, then its dielectric constant $K$ is given by
A parallel-plate capacitor of area $A,$ plate separation $d$ and capacitance $C$ is filled with four dielectric materials having dielectric constants $K_1,K_2,K_3$ and $K_4$ as shown in the figure. If a single dielectric material is to be used to have the same capacitance $C$ in this capacitor, then its dielectric constant $K$ is given by
- [NEET 2016]
