A girl riding a bicycle with a speed of $5\,ms^{-1}$ towards north direction, observes rain falling vertically down. If she increases her speed to $10\,ms^{-1}$, rain appears to meet her at $45^o$ to the vertical. What is the speed of the rain ? In what direction does rain fall as observed by a ground based observer ?

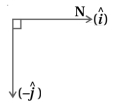
Assume north to be $\hat{i}$ direction and vertically downward to be $\hat{j}$.

Let the rain velocity,

$v_{t}$, be $a \hat{i}+b \hat{j}$

$v_{r}=a \hat{i}+b \hat{j}$

Case $1:$ Given velocity of girl

Let $v_{r g}=$ Velocity of rain w.r.t. girl

$=v_{g}=(5 \mathrm{~m} / \mathrm{s}) \hat{i}$

$=(a-5) \hat{i}+b \hat{j}$

According to question rain, appears to fall vertically downward, Hence, $a-5=0 \Rightarrow a=5$

Case $2:$ Given velocity of the girl,

$v_{g}=(10 \mathrm{~m} / \mathrm{s}) \hat{i}$

$\therefore v_{r g}=v_{r}-v_{g}$

$\quad=(a \hat{i}+b \hat{j})-10 \hat{i}=(a-10) \hat{i}+b \hat{j}$

According to question rain appears to fall at $45^{\circ}$ to the vertical hence $\tan 45^{\circ}=\frac{b}{a-10}=1$

$\Rightarrow b=a-10=5-10=-5$

Hence, velocity of rain $=a \hat{i}+b \hat{j}$

$\Rightarrow v_{r}=5 \hat{i}-5 \hat{j}$

Speed of rain,

$\left|v_{r}\right|=\sqrt{(5)^{2}+(-5)^{2}}=\sqrt{50}=5 \sqrt{2} \mathrm{~m} / \mathrm{s}$