A car $P$ approaching a crossing at a speed of $10\, m/s$ sounds a horn of frequency $700\, Hz$ when $40\, m$ in front of the crossing. Speed of sound in air is $340\, m/s$. Another car $Q$ is at rest on a road which is perpendicular to the road on which car $P$ is reaching the crossing (see figure). The driver of car $Q$ hears the sound of the horn of car $P$ when he is $30\, m$ in front of the crossing. The apparent frequency heard by the driver of car $Q$ is .... $Hz$
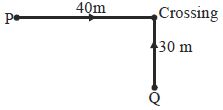
A car $P$ approaching a crossing at a speed of $10\, m/s$ sounds a horn of frequency $700\, Hz$ when $40\, m$ in front of the crossing. Speed of sound in air is $340\, m/s$. Another car $Q$ is at rest on a road which is perpendicular to the road on which car $P$ is reaching the crossing (see figure). The driver of car $Q$ hears the sound of the horn of car $P$ when he is $30\, m$ in front of the crossing. The apparent frequency heard by the driver of car $Q$ is .... $Hz$

- A
$700$
- B
$717$
- C
$1000$
- D
$679$
Similar Questions
The pattern of standing waves formed on a stretched string at two instants of time (extreme, mean) are shown in figure. The velocity of two waves superimposing to form stationary waves is $360\, ms^{-1}$ and their frequencies are $256\, Hz$. Which is not possible value of $t$ (in $\sec$) :-
The pattern of standing waves formed on a stretched string at two instants of time (extreme, mean) are shown in figure. The velocity of two waves superimposing to form stationary waves is $360\, ms^{-1}$ and their frequencies are $256\, Hz$. Which is not possible value of $t$ (in $\sec$) :-
Calculate the temperature at which the speed of sound will be two times its ..... $K$ value at $0\,^oC$
Calculate the temperature at which the speed of sound will be two times its ..... $K$ value at $0\,^oC$
The phase difference between two points separated by $0.8 m$ in a wave of frequency $120 Hz$ is ${90^o}$. Then the velocity of wave will be ............ $\mathrm{m/s}$
The phase difference between two points separated by $0.8 m$ in a wave of frequency $120 Hz$ is ${90^o}$. Then the velocity of wave will be ............ $\mathrm{m/s}$
A string of mass $m$ and length $l$ hangs from ceiling as shown in the figure. Wave in string moves upward. $v_A$ and $v_B$ are the speeds of wave at $A$ and $B$ respectively. Then $v_B$ is
A string of mass $m$ and length $l$ hangs from ceiling as shown in the figure. Wave in string moves upward. $v_A$ and $v_B$ are the speeds of wave at $A$ and $B$ respectively. Then $v_B$ is
A train is moving towards a stationary observer. Which of the following curve best represents the frequency received by observer $f$ as a function of time ?
A train is moving towards a stationary observer. Which of the following curve best represents the frequency received by observer $f$ as a function of time ?
