Three rods $A, B$ and $C$ of thermal conductivities $K, 2\,K$ and $4\,K$, cross-sectional areas $A, 2\,A$ and $2\,A$ and lengths $2l, l$ and $l$ respectively are connected as shown in the figure. If the ends of the rods are maintained at temperatures $100^o\,C, 50^o\,C$, and $0^o\,C$ respectively, then the temperature $\theta$ of the junction is ......... $^oC$
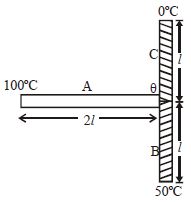
Three rods $A, B$ and $C$ of thermal conductivities $K, 2\,K$ and $4\,K$, cross-sectional areas $A, 2\,A$ and $2\,A$ and lengths $2l, l$ and $l$ respectively are connected as shown in the figure. If the ends of the rods are maintained at temperatures $100^o\,C, 50^o\,C$, and $0^o\,C$ respectively, then the temperature $\theta$ of the junction is ......... $^oC$

- A
$\frac{300}{7}$
- B
$20$
- C
$\frac{200}{7}$
- D
$\frac{200}{13} $
Similar Questions
Two spheres of different materials one with double the radius and one-fourth wall thickness of the other, are filled with ice. If the time taken for complete melting ice in the large radius one is $25$ minutes and that for smaller one is $16$ minutes, the ratio of thermal conductivities of the materials of larger sphere to the smaller sphere is
Two spheres of different materials one with double the radius and one-fourth wall thickness of the other, are filled with ice. If the time taken for complete melting ice in the large radius one is $25$ minutes and that for smaller one is $16$ minutes, the ratio of thermal conductivities of the materials of larger sphere to the smaller sphere is
An ice box used for keeping eatable cold has a total wall area of $1\;metr{e^2}$ and a wall thickness of $5.0cm$. The thermal conductivity of the ice box is $K = 0.01\;joule/metre{ - ^o}C$. It is filled with ice at ${0^o}C$ along with eatables on a day when the temperature is $30°C$ . The latent heat of fusion of ice is $334 \times {10^3}joules/kg$. The amount of ice melted in one day is ........ $gms$ ($1day = 86,400\;\sec onds$)
An ice box used for keeping eatable cold has a total wall area of $1\;metr{e^2}$ and a wall thickness of $5.0cm$. The thermal conductivity of the ice box is $K = 0.01\;joule/metre{ - ^o}C$. It is filled with ice at ${0^o}C$ along with eatables on a day when the temperature is $30°C$ . The latent heat of fusion of ice is $334 \times {10^3}joules/kg$. The amount of ice melted in one day is ........ $gms$ ($1day = 86,400\;\sec onds$)
Six wire each of cross-sectional area $A$ and length $l$ are combined as shown in the figure. The thermal conductivities of copper and iron are $K_1$ and $K_2$ respectively. The equivalent thermal resistance between points $A$ and $C$ is :-
Six wire each of cross-sectional area $A$ and length $l$ are combined as shown in the figure. The thermal conductivities of copper and iron are $K_1$ and $K_2$ respectively. The equivalent thermal resistance between points $A$ and $C$ is :-
Three rods of same material, same area of crosssection but different lengths $10 \,cm , 20 \,cm$ and $30 \,cm$ are connected at a point as shown. What is temperature of junction $O$ is ......... $^{\circ} C$
Three rods of same material, same area of crosssection but different lengths $10 \,cm , 20 \,cm$ and $30 \,cm$ are connected at a point as shown. What is temperature of junction $O$ is ......... $^{\circ} C$
A slab of stone of area $0.36\;m ^2$ and thickness $0.1 \;m$ is exposed on the lower surface to steam at $100^{\circ} C$. A block of ice at $0^{\circ} C$ rests on the upper surface of the slab. In one hour $4.8\; kg$ of ice is melted. The thermal conductivity of slab is .......... $J / m / s /{ }^{\circ} C$ (Given latent heat of fusion of ice $=3.36 \times 10^5\; J kg ^{-1}$)
A slab of stone of area $0.36\;m ^2$ and thickness $0.1 \;m$ is exposed on the lower surface to steam at $100^{\circ} C$. A block of ice at $0^{\circ} C$ rests on the upper surface of the slab. In one hour $4.8\; kg$ of ice is melted. The thermal conductivity of slab is .......... $J / m / s /{ }^{\circ} C$ (Given latent heat of fusion of ice $=3.36 \times 10^5\; J kg ^{-1}$)
- [AIPMT 2012]
