यहाँ आरेख में कुछ समविभव क्षेत्र दर्शाये गये हैं :
प्रत्येक आरेख एक धनात्मक आवेश को $A$ से $B$ तक ले जाते हैं। तो, इस प्रक्रम में, $q$ को $A$ से $B$ तक ले जाने में :
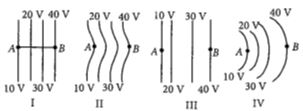
यहाँ आरेख में कुछ समविभव क्षेत्र दर्शाये गये हैं :
प्रत्येक आरेख एक धनात्मक आवेश को $A$ से $B$ तक ले जाते हैं। तो, इस प्रक्रम में, $q$ को $A$ से $B$ तक ले जाने में :

- [NEET 2017]
- A
सभी चारों आरेखों में समान कार्य करना पडेगा
- B
आरेख $(a)$ में न्यूनतम कार्य करना पड़ेगा
- C
आरेख $(b)$ में अधिकतम कार्य करना पड़ेगा
- D
आरेख $(c)$ में अधिकतम कार्य करना पड़ेगा
Similar Questions
समरूप विद्युत क्षेत्र किसी क्षेत्र में धनात्मक $x$-दिशा की ओर इंगित है। माना $A$ मूलबिन्दु है, $B$, $x$-अक्ष पर $x = + 1$ सेमी. पर बिन्दु है तथा $C$ $y$-अक्ष पर $y = + 1$ सेमी. पर एक बिन्दु है तो बिन्दुओं $A$, $B$ व $C$ पर विभव निम्न सम्बंध से सन्तुष्ट होंगे
समरूप विद्युत क्षेत्र किसी क्षेत्र में धनात्मक $x$-दिशा की ओर इंगित है। माना $A$ मूलबिन्दु है, $B$, $x$-अक्ष पर $x = + 1$ सेमी. पर बिन्दु है तथा $C$ $y$-अक्ष पर $y = + 1$ सेमी. पर एक बिन्दु है तो बिन्दुओं $A$, $B$ व $C$ पर विभव निम्न सम्बंध से सन्तुष्ट होंगे
- [IIT 2001]
नीचे दो कथन दिये गये है : एक को अभिकथन ($A$) तथा दूसरे को कारण $(\mathrm{R})$ से चिन्हित किया गया है। अभिकथन ($A$) : एक समविभव पृष्ठ पर गतिमान एक धनावेश पर वैद्युत क्षेत्र द्वारा किया गया कार्य सदैव शून्य होता है।
कारण ($R$) : वैद्युत बल रेखाएँ सदैव समविभव पृष्ठ के लम्बवत् होती है।
उपरोक्त कथनों के आलोक में नीचे दिये गए विकल्पों में से सबसे उचित उत्तर का चयन कीजिए।
नीचे दो कथन दिये गये है : एक को अभिकथन ($A$) तथा दूसरे को कारण $(\mathrm{R})$ से चिन्हित किया गया है। अभिकथन ($A$) : एक समविभव पृष्ठ पर गतिमान एक धनावेश पर वैद्युत क्षेत्र द्वारा किया गया कार्य सदैव शून्य होता है।
कारण ($R$) : वैद्युत बल रेखाएँ सदैव समविभव पृष्ठ के लम्बवत् होती है।
उपरोक्त कथनों के आलोक में नीचे दिये गए विकल्पों में से सबसे उचित उत्तर का चयन कीजिए।
- [JEE MAIN 2024]
व्यवस्थात्मकतः निम्नलिखित में संगत समविभव पृष्ठ का वर्णन कीजिएः
$(a)$ $Z-$दिशा में अचर विद्युत क्षेत्र
$(b)$ एक क्षेत्र जो एकसमान रूप से बढ़ता है, परंतु एक ही दिशा ( मान लीजिए $z-$ दिशा) में रहता है।
$(c)$ मूल बिंदु पर कोई एकल धनावेश, और
$(d)$ एक समतल में समान दूरी पर समांतर लंबे आवेशित तारों से बने एकसमान जाल।
व्यवस्थात्मकतः निम्नलिखित में संगत समविभव पृष्ठ का वर्णन कीजिएः
$(a)$ $Z-$दिशा में अचर विद्युत क्षेत्र
$(b)$ एक क्षेत्र जो एकसमान रूप से बढ़ता है, परंतु एक ही दिशा ( मान लीजिए $z-$ दिशा) में रहता है।
$(c)$ मूल बिंदु पर कोई एकल धनावेश, और
$(d)$ एक समतल में समान दूरी पर समांतर लंबे आवेशित तारों से बने एकसमान जाल।
एक अनन्त कुचालक चादर के एक सतह पर आवेश घनत्व $\sigma = 0.10\, \mu C/m^2$ है। यदि इसके विद्युत क्षेत्र में दो समविभवी सतहों के मध्य विभवान्तर $50\, V$ है तो इनके मध्य की दूरी होगी
एक अनन्त कुचालक चादर के एक सतह पर आवेश घनत्व $\sigma = 0.10\, \mu C/m^2$ है। यदि इसके विद्युत क्षेत्र में दो समविभवी सतहों के मध्य विभवान्तर $50\, V$ है तो इनके मध्य की दूरी होगी
$6\, cm$ की दूरी पर अवस्थित दो बिंदुओं $A$ एवं $B$ पर दो आवेश $2 \mu C$ तथा $-2 \mu C$ रखे हैं।
$(a)$ निकाय के सम विभव पृष्ठ की पहचान कीजिए।
$(b)$ इस पृष्ठ के प्रत्येक बिंदु पर विध्यूत क्षेत्र की दिशा क्या है?
$6\, cm$ की दूरी पर अवस्थित दो बिंदुओं $A$ एवं $B$ पर दो आवेश $2 \mu C$ तथा $-2 \mu C$ रखे हैं।
$(a)$ निकाय के सम विभव पृष्ठ की पहचान कीजिए।
$(b)$ इस पृष्ठ के प्रत्येक बिंदु पर विध्यूत क्षेत्र की दिशा क्या है?
