Represent geometrically numbers on the number line:
$\sqrt{8.1}$
Represent geometrically numbers on the number line:
$\sqrt{8.1}$
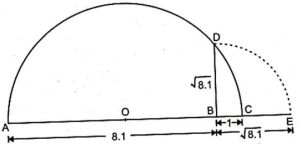
Mark the distance $8.1$ units from a fixed point $A$ on a given line to obtain a point $B$ such that $AB =8.1$ units. From $B$, mark a distance of $1$ unit and mark the new points as $C$. Find the mid-point of $AC$ and mark that point as $0 .$ Draw a semicircle with centre $O$ and radius $OC.$ Draw a line perpendicular to $AC$ passing through $B$ and intersecting the semicircle at $D.$ Then, $B D=\sqrt{8.1}$.
Now, draw an arc with centre $B$ and radius $BD$, which intersects the number line in $E$. Thus, E represents $\sqrt{8.1}$
Similar Questions
Simplify the following:
$4 \sqrt{12} \times 7 \sqrt{6}$
Simplify the following:
$4 \sqrt{12} \times 7 \sqrt{6}$
If $x=7-4 \sqrt{3},$ then find the value of $x^{2}+\frac{1}{x^{2}}$
If $x=7-4 \sqrt{3},$ then find the value of $x^{2}+\frac{1}{x^{2}}$
Is $\sqrt{8+15}$ a rational number or an irrational number ?
Is $\sqrt{8+15}$ a rational number or an irrational number ?
For each question, select the proper option from four options given, to make the statement true : (Final answer only)
The rationalising factor of $4-\sqrt{5}$ is...........
For each question, select the proper option from four options given, to make the statement true : (Final answer only)
The rationalising factor of $4-\sqrt{5}$ is...........
Rationalise the denominator in each of the following
$\frac{1}{\sqrt{5}-\sqrt{3}}$
Rationalise the denominator in each of the following
$\frac{1}{\sqrt{5}-\sqrt{3}}$


