An infinitely long conductor $PQR$ is bent to form a right angle as shown. A current $I$ flows through $PQR$ The magnetic field due to this current at the point $M $ is $H_1$. Now another infinitely long straight conductor $QS$ is connected at $Q$ so that the current is $I/2$ in $QR$ as well as in $QS$, The current in $PQ$ remaining unchanged. The magnetic field at $M$ is now ${H_{2.}}$The ratio ${H_1}/{H_2}$ is given by
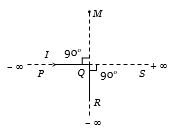
An infinitely long conductor $PQR$ is bent to form a right angle as shown. A current $I$ flows through $PQR$ The magnetic field due to this current at the point $M $ is $H_1$. Now another infinitely long straight conductor $QS$ is connected at $Q$ so that the current is $I/2$ in $QR$ as well as in $QS$, The current in $PQ$ remaining unchanged. The magnetic field at $M$ is now ${H_{2.}}$The ratio ${H_1}/{H_2}$ is given by

- [IIT 2000]
- A
$0.5$
- B
$1$
- C
$0.67$
- D
$2$
Similar Questions
Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field $B_1,$ at its centre when a current $I$ passes through it.The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field $B_2$ at the centre of the loops when current $I/3$ passes through it. The ratio $B_1 : B_2$ is
Consider two thin identical conducting wires covered with very thin insulating material. One of the wires is bent into a loop and produces magnetic field $B_1,$ at its centre when a current $I$ passes through it.The second wire is bent into a coil with three identical loops adjacent to each other and produces magnetic field $B_2$ at the centre of the loops when current $I/3$ passes through it. The ratio $B_1 : B_2$ is
- [JEE MAIN 2014]
In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$. Net magnetic field at centre will be
In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$. Net magnetic field at centre will be
- [KVPY 2012]
A regular polygon of $6$ sides is formed by bending
a wire of length $4 \pi$ meter. If an electric current of $4 \pi \sqrt{3} \mathrm{~A}$ is flowing through the sides of the polygon, the magnetic field at the centre of the polygon would be $x \times 10^{7} \mathrm{~T}$. The value of $\mathrm{x}$ is______.
A regular polygon of $6$ sides is formed by bending
a wire of length $4 \pi$ meter. If an electric current of $4 \pi \sqrt{3} \mathrm{~A}$ is flowing through the sides of the polygon, the magnetic field at the centre of the polygon would be $x \times 10^{7} \mathrm{~T}$. The value of $\mathrm{x}$ is______.
- [JEE MAIN 2024]
A circular coil ‘$A$’ has a radius $R$ and the current flowing through it is $I$. Another circular coil ‘$B$’ has a radius $2R$ and if $2I$ is the current flowing through it, then the magnetic fields at the centre of the circular coil are in the ratio of (i.e.${B_A}$ to ${B_B}$)
A circular coil ‘$A$’ has a radius $R$ and the current flowing through it is $I$. Another circular coil ‘$B$’ has a radius $2R$ and if $2I$ is the current flowing through it, then the magnetic fields at the centre of the circular coil are in the ratio of (i.e.${B_A}$ to ${B_B}$)
- [AIEEE 2002]
Which of the following statements regarding magnetic lines of force is correct?
Which of the following statements regarding magnetic lines of force is correct?
