A thin flexible wire of length $\mathrm{L}$ is connected to two adjacent fixed points and carries a current $\mathrm{I}$ in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength $B$ going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is
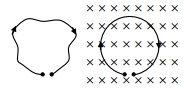
A thin flexible wire of length $\mathrm{L}$ is connected to two adjacent fixed points and carries a current $\mathrm{I}$ in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength $B$ going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is

- [IIT 2010]
- A
$IBL$
- B
$\frac{\mathrm{IBL}}{\pi}$
- C
$\frac{\mathrm{IBL}}{2 \pi}$
- D
$\frac{\mathrm{IBL}}{4 \pi}$
Similar Questions
A $3.0\; cm$ wire carrying a current of $10 \;A$ is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be $0.27\; T$. What is the magnetic force on the wire?
A $3.0\; cm$ wire carrying a current of $10 \;A$ is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be $0.27\; T$. What is the magnetic force on the wire?
Two straight parallel wires, both carrying $10$ $ampere$ in the same direction attract each other with a force of $1 \times {10^{ - 3}}\,N$. If both currents are doubled, the force of attraction will be
Two straight parallel wires, both carrying $10$ $ampere$ in the same direction attract each other with a force of $1 \times {10^{ - 3}}\,N$. If both currents are doubled, the force of attraction will be
A square loop $ABCD$, carrying a current $i,$ is placed near and coplanar with a long straight conductor $XY$ carrying a current $I,$ the net force on the loop will be
A square loop $ABCD$, carrying a current $i,$ is placed near and coplanar with a long straight conductor $XY$ carrying a current $I,$ the net force on the loop will be
The resultant force on the current loop $PQRS$ due to a long current carrying conductor will be
The resultant force on the current loop $PQRS$ due to a long current carrying conductor will be
A semi circular current carrying wire having radius $R$ is placed in $x-y$ plane with its centre at origin $‘O’$. There is non-uniform magnetic $\vec B = \frac{{{B_o}x}}{{2R}}\hat k$ (here $B_o$ is + $ve$ constant) is existing in the region. The magnetic force acting on semi circular wire will be along
A semi circular current carrying wire having radius $R$ is placed in $x-y$ plane with its centre at origin $‘O’$. There is non-uniform magnetic $\vec B = \frac{{{B_o}x}}{{2R}}\hat k$ (here $B_o$ is + $ve$ constant) is existing in the region. The magnetic force acting on semi circular wire will be along
