A projectile is launched from the origin in the $xy$ plane ( $x$ is the horizontal and $y$ is the vertically up direction) making an angle $\alpha$ from the $x$-axis. If its distance. $r =\sqrt{ x ^2+ y ^2}$ from the origin is plotted against $x$, the resulting curves show different behaviours for launch angles $\alpha_1$ and $\alpha_2$ as shown in the figure below. For $\alpha_1, r ( x )$ keeps increasing with $x$ while for $\alpha_2$, $r(x)$ increases and reaches a maximum, then decreases and goes through a minimum before increasing again. The switch between these two cases takes place at an angle $\alpha_c\left(\alpha_1 < \alpha_c < \alpha_2\right)$. The value of $\alpha_c$ is [ignore where $v_0$ is the initial speed of the projectile and $g$ is the acceleration due to gravity]
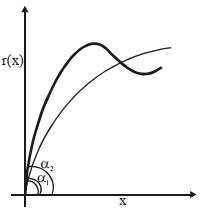
A projectile is launched from the origin in the $xy$ plane ( $x$ is the horizontal and $y$ is the vertically up direction) making an angle $\alpha$ from the $x$-axis. If its distance. $r =\sqrt{ x ^2+ y ^2}$ from the origin is plotted against $x$, the resulting curves show different behaviours for launch angles $\alpha_1$ and $\alpha_2$ as shown in the figure below. For $\alpha_1, r ( x )$ keeps increasing with $x$ while for $\alpha_2$, $r(x)$ increases and reaches a maximum, then decreases and goes through a minimum before increasing again. The switch between these two cases takes place at an angle $\alpha_c\left(\alpha_1 < \alpha_c < \alpha_2\right)$. The value of $\alpha_c$ is [ignore where $v_0$ is the initial speed of the projectile and $g$ is the acceleration due to gravity]

- [KVPY 2021]
- A
$\sin ^{-1}\left(\frac{1}{3}\right)$
- B
$\cos ^{-1}\left(\frac{1}{3}\right)$
- C
$\tan ^{-1}\left(\frac{1}{3}\right)$
- D
$\tan ^{-1}(3)$
Similar Questions
A shell fired from the base of a mountain just clears it. If $\alpha$ is the angle of projection then the angular elevation of the summit $\beta$ is
A shell fired from the base of a mountain just clears it. If $\alpha$ is the angle of projection then the angular elevation of the summit $\beta$ is
Two projectiles, one fired from surface of earth with velocity $10 \,m/s$ and other fired from the surface of another planet with initial speed $5\, m/s$ trace identical trajectories. The value of acceleration due to the gravity on the planet is ......... $m/s^2$
Two projectiles, one fired from surface of earth with velocity $10 \,m/s$ and other fired from the surface of another planet with initial speed $5\, m/s$ trace identical trajectories. The value of acceleration due to the gravity on the planet is ......... $m/s^2$
Range of a bob of mass $1\, kg$ is $80\,m$ while it attains maximum height $20\,m$. Its change in momentum in complete motion ............ $N-s$
Range of a bob of mass $1\, kg$ is $80\,m$ while it attains maximum height $20\,m$. Its change in momentum in complete motion ............ $N-s$
A projectile is fired with a speed $u$ at an angle $\theta$ with the horizontal. Its speed when its direction of motion makes an angle ‘$\alpha $’ with the horizontal is
A projectile is fired with a speed $u$ at an angle $\theta$ with the horizontal. Its speed when its direction of motion makes an angle ‘$\alpha $’ with the horizontal is
If a body $A$ of mass $M$ is thrown with velocity $v$ at an angle of ${30^o}$ to the horizontal and another body $B$ of the same mass is thrown with the same speed at an angle of ${60^o}$ to the horizontal. The ratio of horizontal range of $A$ to $B$ will be
If a body $A$ of mass $M$ is thrown with velocity $v$ at an angle of ${30^o}$ to the horizontal and another body $B$ of the same mass is thrown with the same speed at an angle of ${60^o}$ to the horizontal. The ratio of horizontal range of $A$ to $B$ will be
- [AIPMT 1992]
