A particle is moving eastwards with a speed of $6 \,m / s$. After $6 \,s$, the particle is found to be moving with same speed in a direction $60^{\circ}$ north of east. The magnitude of average acceleration in this interval of time is ....... $m / s ^2$
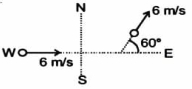
A particle is moving eastwards with a speed of $6 \,m / s$. After $6 \,s$, the particle is found to be moving with same speed in a direction $60^{\circ}$ north of east. The magnitude of average acceleration in this interval of time is ....... $m / s ^2$

- A
$6$
- B
$3$
- C
$1$
- D
$0$
Similar Questions
A particle moves such that its position vector $\overrightarrow{\mathrm{r}}(\mathrm{t})=\cos \omega \mathrm{t} \hat{\mathrm{i}}+\sin \omega \mathrm{t} \hat{\mathrm{j}}$ where $\omega$ is a constant and $t$ is time. Then which of the following statements is true for the velocity $\overrightarrow{\mathrm{v}}(\mathrm{t})$ and acceleration $\overrightarrow{\mathrm{a}}(\mathrm{t})$ of the particle
A particle moves such that its position vector $\overrightarrow{\mathrm{r}}(\mathrm{t})=\cos \omega \mathrm{t} \hat{\mathrm{i}}+\sin \omega \mathrm{t} \hat{\mathrm{j}}$ where $\omega$ is a constant and $t$ is time. Then which of the following statements is true for the velocity $\overrightarrow{\mathrm{v}}(\mathrm{t})$ and acceleration $\overrightarrow{\mathrm{a}}(\mathrm{t})$ of the particle
- [JEE MAIN 2020]
A particle starting from the origin $(0, 0)$ moves in a straight line in the $(x, y)$ plane. Its coordinates at a later time are $(\sqrt 3 , 3) .$ The path of the particle makes with the $x-$axis an angle of ......... $^o$
- [AIPMT 2007]
A particle starts moving rectilinearly at time $t = 0$ such that its velocity $'v'$ changes with time $'t'$ according to the equation $v = t^2 - t$ where $t$ is in seconds and $v$ is in $m/s.$ The time interval for which the particle retards is
A particle starts moving rectilinearly at time $t = 0$ such that its velocity $'v'$ changes with time $'t'$ according to the equation $v = t^2 - t$ where $t$ is in seconds and $v$ is in $m/s.$ The time interval for which the particle retards is
The position of a particle moving in the $xy-$plane at any time $t$ is given by $x = (3{t^2} - 6t)$ metres, $y = ({t^2} - 2t)$ metres. Select the correct statement about the moving particle from the following
The position of a particle moving in the $xy-$plane at any time $t$ is given by $x = (3{t^2} - 6t)$ metres, $y = ({t^2} - 2t)$ metres. Select the correct statement about the moving particle from the following
