A parallel plate condenser is filled with two dielectrics as shown. Area of each plate is $A\;metr{e^2}$ and the separation is $t$ $metre$. The dielectric constants are ${k_1}$ and ${k_2}$ respectively. Its capacitance in farad will be
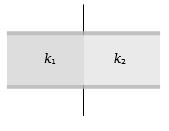
A parallel plate condenser is filled with two dielectrics as shown. Area of each plate is $A\;metr{e^2}$ and the separation is $t$ $metre$. The dielectric constants are ${k_1}$ and ${k_2}$ respectively. Its capacitance in farad will be

- [AIIMS 2001]
- A
$\frac{{{\varepsilon _0}A}}{t}({k_1} + {k_2})$
- B
$\frac{{{\varepsilon _0}A}}{t}.\frac{{{k_1} + {k_2}}}{2}$
- C
$\frac{{2{\varepsilon _0}A}}{t}({k_1} + {k_2})$
- D
$\frac{{{\varepsilon _0}A}}{t}.\frac{{{k_1} - {k_2}}}{2}$
Similar Questions
A dielectric slab of thickness $d$ is inserted in a parallel plate capacitor whose negative plate is at $x = 0$ and positive plate is at $x = 3d$. The slab is equidistant from the plates. The capacitor is given some charge. As one goes from $0$ to $3d$
A dielectric slab of thickness $d$ is inserted in a parallel plate capacitor whose negative plate is at $x = 0$ and positive plate is at $x = 3d$. The slab is equidistant from the plates. The capacitor is given some charge. As one goes from $0$ to $3d$
- [IIT 1998]
The plates of a parallel plate capacitor are charged up to $100\, volt$. A $2\, mm$ thick plate is inserted between the plates, then to maintain the same potential difference, the distance between the capacitor plates is increased by $1.6\, mm$. The dielectric constant of the plate is
The plates of a parallel plate capacitor are charged up to $100\, volt$. A $2\, mm$ thick plate is inserted between the plates, then to maintain the same potential difference, the distance between the capacitor plates is increased by $1.6\, mm$. The dielectric constant of the plate is
A parallel plate capacitor of capacitance $90\ pF$ is connected to a battery of $emf$ $20\ V$. If a dielectric material of dielectric constant $K = \frac{5}{3}$ is inserted between the plates, the magnitude of the induced charge will be.......$n $ $C$
A parallel plate capacitor of capacitance $90\ pF$ is connected to a battery of $emf$ $20\ V$. If a dielectric material of dielectric constant $K = \frac{5}{3}$ is inserted between the plates, the magnitude of the induced charge will be.......$n $ $C$
- [JEE MAIN 2018]
The capacitance of a parallel plate capacitor is $5\, \mu F$ . When a glass slab of thickness equal to the separation between the plates is introduced between the plates, the potential difference reduces to $1/8$ of the original value. The dielectric constant of glass is
The capacitance of a parallel plate capacitor is $5\, \mu F$ . When a glass slab of thickness equal to the separation between the plates is introduced between the plates, the potential difference reduces to $1/8$ of the original value. The dielectric constant of glass is
A capacitor of capacitance $9 n F$ having dielectric slab of $\varepsilon_{ r }=2.4$ dielectric strength $20\, MV / m$ and $P.D. =20 \,V$ then area of plates is ....... $\times 10^{-4}\, m ^{2}$
A capacitor of capacitance $9 n F$ having dielectric slab of $\varepsilon_{ r }=2.4$ dielectric strength $20\, MV / m$ and $P.D. =20 \,V$ then area of plates is ....... $\times 10^{-4}\, m ^{2}$
- [AIIMS 2019]
