Two long straight conductors with currents I_ | vedclass

Name: PDF Generator App | JEE NEET Paper Generator | Vedclass
Brand: Vedclass
Rating: 5 (35 reviews)

Question

magnetic field $B=\frac{\mu_{0} I}{2 \pi r}$

the magnetic field at any point in the $xy$ plane $B=\frac{\mu_{0} I_{1}}{2 \pi y}-\frac{\mu_{0} I_{2}

Vedclass · Accepted Answer

$Y = \frac{{{I_1}}}{{{I_2}}}\,X$

Vedclass · Answer

magnetic field $B=\frac{\mu_{0} I}{2 \pi r}$

the magnetic field at any point in the $xy$ plane $B=\frac{\mu_{0} I_{1}}{2 \pi y}-\frac{\mu_{0} I_{2}}{2 \pi x}$

(assuming current flowing in $x$ and $y$$-direction$ respectively.)

So, the equation of the locus of zero magnetic induction,

$\frac{I_{1}}{y}=\frac{I_{2}}{x}$

$y=\frac{I_{1} x}{I_{2}}$

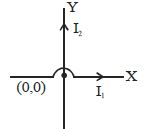
Two long straight conductors with currents $I_1$ and $I_2$ are placed along $X$ and $Y-$ axes. The equation of locus of points of zero magnetic induction is

Similar Questions

Magnetic field due to $0.1\, A$ current flowing through a circular coil of radius $0.1\, m$ and $1000$ $turns$ at the centre of the coil is

When equal current is passed through two coils, equal magnetic field is produced at their centres. If the ratio of number of turns in the coils is $8: 15$, then the ratio of their radii will be

An electron moving in a circular orbit of radius $r$ makes $n$ rotation per second. The magnetic field produced at the centre has a magnitude of

A part of a long wire carrying a current $i$ is bent into a circle of radius $r$ as shown in figure. The net magnetic field at the centre $O$ of the circular loop is

A wire carrying current $I$ has the shape as shown in adjoining figure.Linear parts of the wire are very long and parallel to $X-$axis while semicircular portion of radius $R$ is lying in $Y-Z$ plane. Magnetic field at point $O$ is