चित्र में, एक काँच नलिका (रेखीय प्रसार गुणांक $\alpha$) में एक द्रव ऊपर तक भरा हुआ है जिसका आयतन प्रसार गुणांक $\gamma$ है। गर्म करने पर द्रव स्तम्भ की लम्बाई अपरिवर्तित रहती है। $\gamma$ एवं $\alpha$ के बीच सही सम्बन्ध है
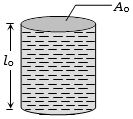
चित्र में, एक काँच नलिका (रेखीय प्रसार गुणांक $\alpha$) में एक द्रव ऊपर तक भरा हुआ है जिसका आयतन प्रसार गुणांक $\gamma$ है। गर्म करने पर द्रव स्तम्भ की लम्बाई अपरिवर्तित रहती है। $\gamma$ एवं $\alpha$ के बीच सही सम्बन्ध है

- A
$\gamma=\alpha$
- B
$\gamma= 2\alpha$
- C
$\gamma= 3\alpha$
- D
$\gamma = \frac{\alpha }{3}$
Similar Questions
एक काँच पात्र में मरकरी का आभासी प्रसार गुणांक $153 \times 10{^{-6}}{°C^{-1}}$ एवं स्टील पात्र में मरकरी का आभासी प्रसार गुणांक $144 \times 10{^{-6}}{°C^{-1}}$ है। यदि स्टील के लिए a का मान $12 × 10 {^{-6}}{°C^{-1}}$ हो, तब ग्लास के लिए $\alpha$ का मान होगा
एक काँच पात्र में मरकरी का आभासी प्रसार गुणांक $153 \times 10{^{-6}}{°C^{-1}}$ एवं स्टील पात्र में मरकरी का आभासी प्रसार गुणांक $144 \times 10{^{-6}}{°C^{-1}}$ है। यदि स्टील के लिए a का मान $12 × 10 {^{-6}}{°C^{-1}}$ हो, तब ग्लास के लिए $\alpha$ का मान होगा
$0.1 kg$ की एक स्टील गेंद $10 m$ की ऊँचाई से स्वतंत्रतापूर्वक पृथ्वी तल पर गिरती है एवं तल से $5.4m$ ऊँचाई, तक उछलती है। यदि इस प्रक्रिया में व्यय ऊर्जा गेंद द्वारा अवशोषित कर ली जाती है तब इसके ताप मे वृद्धि ........... $^\circ \mathrm{C}$ होगी(स्टील की विशिष्ट ऊष्मा $ = 460\,Joule - k{g^{ - 1}}^\circ {C^{ - 1}},\;g = 10\,m{s^{ - 2}}$)
$0.1 kg$ की एक स्टील गेंद $10 m$ की ऊँचाई से स्वतंत्रतापूर्वक पृथ्वी तल पर गिरती है एवं तल से $5.4m$ ऊँचाई, तक उछलती है। यदि इस प्रक्रिया में व्यय ऊर्जा गेंद द्वारा अवशोषित कर ली जाती है तब इसके ताप मे वृद्धि ........... $^\circ \mathrm{C}$ होगी(स्टील की विशिष्ट ऊष्मा $ = 460\,Joule - k{g^{ - 1}}^\circ {C^{ - 1}},\;g = 10\,m{s^{ - 2}}$)
कैल्विन पैमाने पर किसी वस्तु का ताप $X\,K$ है, यदि इसे फैरेनहाइट पैमाने पर नापा जाए तो यह ${X^o}F$ प्राप्त होता है, $X$ का मान होगा
कैल्विन पैमाने पर किसी वस्तु का ताप $X\,K$ है, यदि इसे फैरेनहाइट पैमाने पर नापा जाए तो यह ${X^o}F$ प्राप्त होता है, $X$ का मान होगा
स्पष्ट कीजिए कि क्यों
$(a)$ अधिक परावर्तकता वाले पिण्ड अल्प उत्सर्जक होते हैं।
$(b)$ कंपकंपी वाले दिन लकड़ी की ट्रे की अपेक्षा पीतल का गिलास कहीं अधिक शीतल प्रतीत होता है।
$(c)$ कोई प्रकाशिक उत्तापमापी (उच्च तापों को मापने की युक्ति), जिसका अंशांकन किसी आदर्श कृष्णिका के विकिरणों के लिए किया गया है, खुले में रखे किसी लाल तप्त लोहे के टुकड़े का ताप काफी कम मापता है, परन्तु जब उसी लोहे के टुकड़े को भट्ठी में रखते हैं, तो वह ताप का सही मान मापता है।
$(d)$ बिना वातावरण के पृथ्वी अशरणीय शीतल हो जाएगी।
$(e)$ भाप के परिचालन पर आधारित तापन निकाय तप्त जल के परिचालन पर आधारित निकायों की अपेक्षा भवनों को उष्ण बनाने में अधिक दक्ष होते हैं।
स्पष्ट कीजिए कि क्यों
$(a)$ अधिक परावर्तकता वाले पिण्ड अल्प उत्सर्जक होते हैं।
$(b)$ कंपकंपी वाले दिन लकड़ी की ट्रे की अपेक्षा पीतल का गिलास कहीं अधिक शीतल प्रतीत होता है।
$(c)$ कोई प्रकाशिक उत्तापमापी (उच्च तापों को मापने की युक्ति), जिसका अंशांकन किसी आदर्श कृष्णिका के विकिरणों के लिए किया गया है, खुले में रखे किसी लाल तप्त लोहे के टुकड़े का ताप काफी कम मापता है, परन्तु जब उसी लोहे के टुकड़े को भट्ठी में रखते हैं, तो वह ताप का सही मान मापता है।
$(d)$ बिना वातावरण के पृथ्वी अशरणीय शीतल हो जाएगी।
$(e)$ भाप के परिचालन पर आधारित तापन निकाय तप्त जल के परिचालन पर आधारित निकायों की अपेक्षा भवनों को उष्ण बनाने में अधिक दक्ष होते हैं।
$50\, K$ पर द्रव ऑक्सीजन को $300\, K$ तक एक $1$ वायुमंडलीय स्थिर दाब पर गर्म किया जाता है। यदि गर्म करने की दर स्थिर है तो, निम्नांकित में से कौन सा ग्राफ (आलेख) समय के साथ ताप के परिवर्तन को प्रदशित करता है ?
$50\, K$ पर द्रव ऑक्सीजन को $300\, K$ तक एक $1$ वायुमंडलीय स्थिर दाब पर गर्म किया जाता है। यदि गर्म करने की दर स्थिर है तो, निम्नांकित में से कौन सा ग्राफ (आलेख) समय के साथ ताप के परिवर्तन को प्रदशित करता है ?
