A train whistling at constant frequency is moving towards a station at a constant speed V . train go

English

Gujarati

Hindi

14.Waves and Sound

normal

A train whistling at constant frequency is moving towards a station at a constant speed $V$. The train goes past a stationary observer on the station. The frequency $n'$ of the sound as heard by the observer is plotted as a function of time $t (Fig.)$ . Identify the expected curve

A

B

C

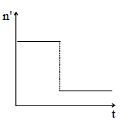
D

Solution

Approaching source $n' = n\left[ {\frac{V}{{V – {V_S}}}} \right]$ constant

Receading source $n' = \left[ {\frac{V}{{V + {V_S}}}} \right]$ constant

Standard 11

Physics

Share

Similar Questions

$y = a\,cos\,(kx -\omega t)$ superposes on another wave giving a stationary wave having node at $x = 0$ . What is the equation of the other wave

normal

A man is watching two trains, one leaving and the other coming with equal speed of $4\,m/s$ . If they sound their whistles each of frequency $240\, Hz$ , the number of beats per sec heard by man will be equal to: (velocity of sound in air $= 320\, m/s$ )

normal

A cylindrical tube $(L = 120\, cm.)$ is resonant with a tuning fork of frequency $330\, Hz$. If it is filling by water then to get resonance again, minimum length of water column is …… $cm$ $(v_{air} = 330\, m/s)$

normal

The diagram shows snapshot of a wave at time $t = 0$. The particle at $x = x_1$ is moving upward at that instant. Direction of propagation of wave is

normal

A string of mass $M$ and length $L$ hangs freely from a fixed point. The velocity of transverse wave along the string at a distance $'x'$ from the free end will be

normal