Two wires of the same material (Young's m | vedclass

Name: PDF Generator App | JEE NEET Paper Generator | Vedclass
Brand: Vedclass
Rating: 5 (35 reviews)

Question

Energy stored $\mathrm{U}=\frac{1}{2} 	imes \frac{(	ext { stress })^{2}}{\mathrm{Y}} 	imes$ volume

$U_{T}=U_{1}+U_{2}$

$=\frac{1}{2 \mathrm{Y}}\l

Vedclass · Accepted Answer

$\frac{{5{W^2}L}}{{8\pi {R^2}Y}}$

Vedclass · Answer

Energy stored $\mathrm{U}=\frac{1}{2} 	imes \frac{(	ext { stress })^{2}}{\mathrm{Y}} 	imes$ volume

$U_{T}=U_{1}+U_{2}$

$=\frac{1}{2 \mathrm{Y}}\left[\left(\frac{\mathrm{W}}{\mathrm{A}_{1}}ight)^{2} 	imes \mathrm{A}_{1} 	imes \mathrm{L}+\left(\frac{\mathrm{W}}{\mathrm{A}_{2}}ight)^{2} 	imes \mathrm{A}_{2} 	imes \mathrm{L}ight]$

$=\frac{W^{2} L}{2 Y}\left[\frac{1}{A_{1}^{2}}+\frac{1}{A_{2}^{2}}ight]$

$=\frac{W^{2} L}{2 Y}\left[\frac{1}{\pi R^{2}}+\frac{1}{\pi(2 R)^{2}}ight]$

$=\frac{W^{2} L}{2 \pi Y R^{2}}\left(1+\frac{1}{4}ight)=\frac{5 W^{2} L}{8 \pi Y R^{2}}$

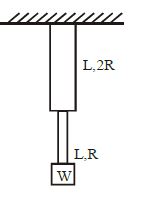
Two wires of the same material (Young's modulus $Y$ ) and same length $L$ but radii $R$ and $2R$ respectively are joined end to end and a weight $W$ is suspended from the combination as shown in the figure. The elastic potential energy in the system is

Similar Questions

Identical springs of steel and copper are equally stretched. On which more work will have to be done ?

The elastic behaviour of material for linear streass and linear strain, is shown in the figure. The energy density for a linear strain of $5 \times 10^{-4}$ is $\dots \; kJ / m ^{3}$. Assume that material is elastic upto the linear strain of $5 \times 10^{-4}$.

A wire of length $L$ and cross-sectional area $A$ is made of a material of Young's modulus $Y.$ It is stretched by an amount $x$. The work done is

The work done in increasing the length of a $1$ $metre$ long wire of cross-section area $1\, mm^2$ through $1\, mm$ will be ....... $J$ $(Y = 2\times10^{11}\, Nm^{-2})$

If $x$ longitudinal strain is produced in a wire of Young's modulus $y,$ then energy stored in the material of the wire per unit volume is