A small body slips, subject to the force of friction, from point $A$ to point $B$ along two curved surfaces of equal radius, first along route $1,$ then along route $2$. Friction does not depend on the speed and the coefficient of friction on both routes is the same. In which case will the body’s speed at $B$ be greater?
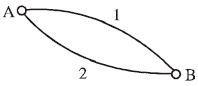
A small body slips, subject to the force of friction, from point $A$ to point $B$ along two curved surfaces of equal radius, first along route $1,$ then along route $2$. Friction does not depend on the speed and the coefficient of friction on both routes is the same. In which case will the body’s speed at $B$ be greater?

- A
speed is greater in case $1$
- B
speed is greater in case $2$
- C
speed is same in both cases
- D
cannot be determined
Similar Questions
A horizontal force $12 \,N$ pushes a block weighing $1/2\, kg$ against a vertical wall. The coefficient of static friction between the wall and the block is $0.5$ and the coefficient of kinetic friction is $0.35.$ Assuming that the block is not moving initially. Which one of the following choices is correct (Take $g = 10 \,m/s^2$)
A horizontal force $12 \,N$ pushes a block weighing $1/2\, kg$ against a vertical wall. The coefficient of static friction between the wall and the block is $0.5$ and the coefficient of kinetic friction is $0.35.$ Assuming that the block is not moving initially. Which one of the following choices is correct (Take $g = 10 \,m/s^2$)
Why are mountain roads generally made winding upwards rather than going straight up ?
Why are mountain roads generally made winding upwards rather than going straight up ?
A block of mass $70\,kg$ is kept on a rough horizontal surface $(\mu = 0.4)$. A person is trying to pull the block by applying a horizontal force, but the block is not moving. The net contact force exerted by the surface on the block is $F$, then
A block of mass $70\,kg$ is kept on a rough horizontal surface $(\mu = 0.4)$. A person is trying to pull the block by applying a horizontal force, but the block is not moving. The net contact force exerted by the surface on the block is $F$, then
The retarding acceleration of $7.35\, ms^{-2}$ due to frictional force stops the car of mass $400\, kg$ travelling on a road. The coefficient of friction between the tyre of the car and the road is
The retarding acceleration of $7.35\, ms^{-2}$ due to frictional force stops the car of mass $400\, kg$ travelling on a road. The coefficient of friction between the tyre of the car and the road is
A force $f$ is acting on a block of mass $m$. Coefficient of friction between block and surface is $\mu$. The block can be pulled along the surface if :-
A force $f$ is acting on a block of mass $m$. Coefficient of friction between block and surface is $\mu$. The block can be pulled along the surface if :-
